The tedious, time-consuming, and buggy nature of system-level simulations is exacerbated with massive MIMO. This post offers some relieve in the form of analytical expressions for downlink conjugate beamforming [1]. These expressions enable the testing and calibration of simulators—say to determine how many cells are needed to represent an infinitely large network with some desired accuracy. The trick that makes the analysis feasible is to let the shadowing grow strong, yet the ensuing expressions capture very well the behaviors with practical shadowings.
The setting is an infinitely large cellular network where each ![]() -antenna base station (BS) serves
-antenna base station (BS) serves ![]() single-antenna users. The large-scale channel gains include pathloss with exponent
single-antenna users. The large-scale channel gains include pathloss with exponent ![]() and shadowing having log-scale standard deviation
and shadowing having log-scale standard deviation ![]() , with the gain between the
, with the gain between the ![]() th BS and the
th BS and the ![]() th user served by a BS of interest denoted by
th user served by a BS of interest denoted by ![]() . With conjugate beamforming and receivers reliant on channel hardening, the signal-to-interference ratio (SIR) at such user is [2]
. With conjugate beamforming and receivers reliant on channel hardening, the signal-to-interference ratio (SIR) at such user is [2]
![]()
where ![]() is the gain from the serving BS and
is the gain from the serving BS and ![]() is the share of that BS’s power allocated to user
is the share of that BS’s power allocated to user ![]() . Two power allocations can be analyzed:
. Two power allocations can be analyzed:
- Uniform:
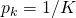 .
. - SIR-equalizing [3]:
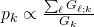 , with the proportionality constant ensuring that
, with the proportionality constant ensuring that 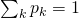 . This makes
. This makes 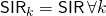 . Moreover, as
. Moreover, as 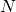 and
and 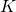 grow large,
grow large, 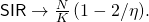
The analysis is conducted for ![]() , which makes it valid for arbitrary BS locations.
, which makes it valid for arbitrary BS locations.
SIR
For notational compactness, let ![]() . Define
. Define ![]() as the solution to
as the solution to ![]() where
where ![]() is the lower incomplete gamma function. For
is the lower incomplete gamma function. For ![]() , in particular,
, in particular, ![]() . Under a uniform power allocation, the CDF of
. Under a uniform power allocation, the CDF of ![]() is available in an explicit form involving the Gauss hypergeometric function
is available in an explicit form involving the Gauss hypergeometric function ![]() (available in MATLAB and Mathematica):
(available in MATLAB and Mathematica):
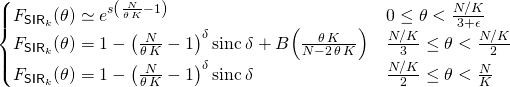
where “![]() ” indicates asymptotic (
” indicates asymptotic (![]() ) equality,
) equality, ![]() is such that the CDF is continuous, and
is such that the CDF is continuous, and
![]()
Alternatively, the CDF can be obtained by solving (e.g., with Mathematica) a single integral involving the Kummer function ![]() :
:
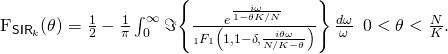
This latter solution can be modified for the SIR-equalizing power allocation as
![]()
Spectral Efficiency
The spectral efficiency of user ![]() is
is ![]() with CDF
with CDF ![]() readily characterizable from the expressions given earlier. From
readily characterizable from the expressions given earlier. From ![]() , the sum spectral efficiency at the BS of interest can be found as
, the sum spectral efficiency at the BS of interest can be found as ![]() Expressions for the averages
Expressions for the averages ![]() and
and ![]() are further available in the form of single integrals.
are further available in the form of single integrals.
With a uniform power allocation,
(1) ![]()
and ![]() . For the special case of
. For the special case of ![]() , the Kummer function simplifies giving
, the Kummer function simplifies giving
(2) ![]()
With an equal-SIR power allocation
(3) ![]()
and ![]() .
.
Application to Relevant Networks
Let us now contrast the analytical expressions (computable instantaneously and exactly, and valid for arbitrary topologies, but asymptotic in the shadowing strength) with some Monte-Carlo simulations (lengthy, noisy, and bug-prone, but for precise shadowing strengths and topologies).
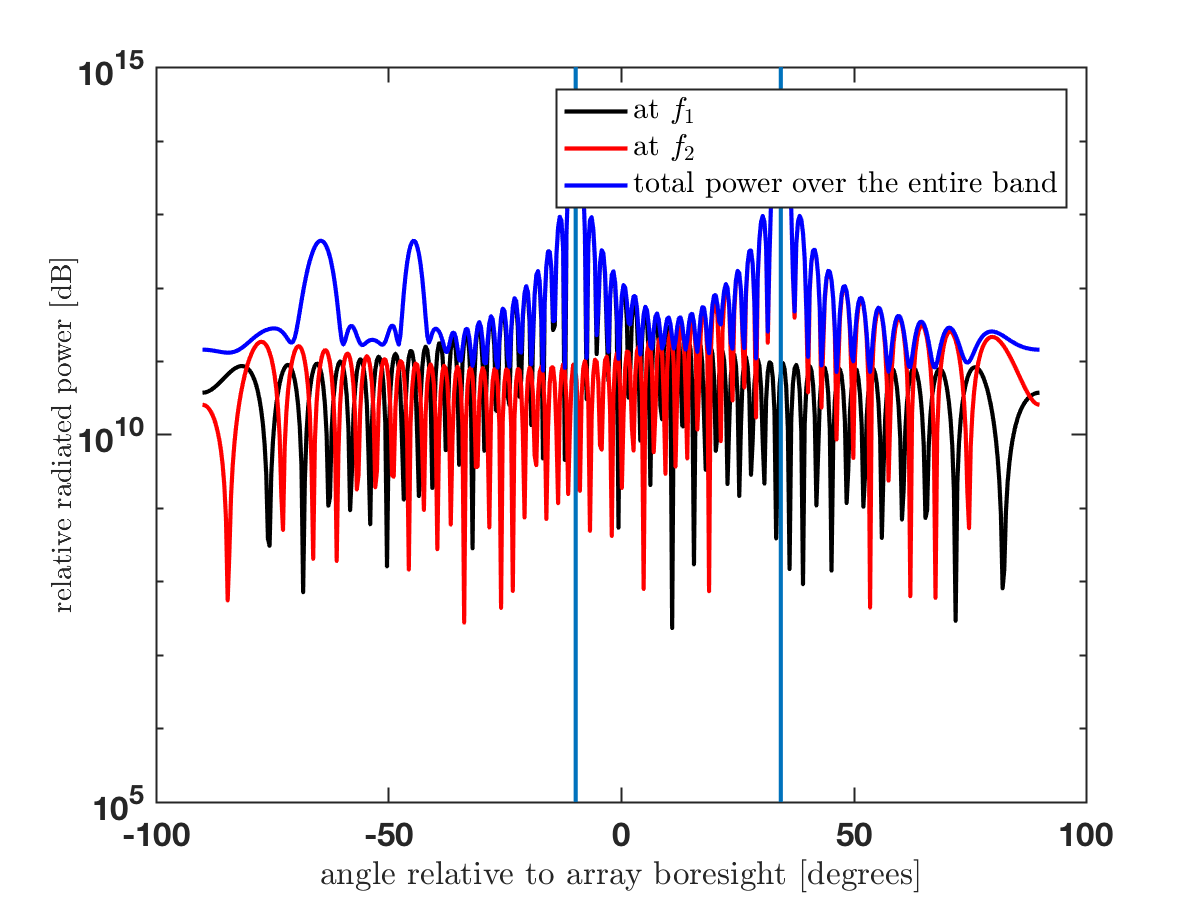
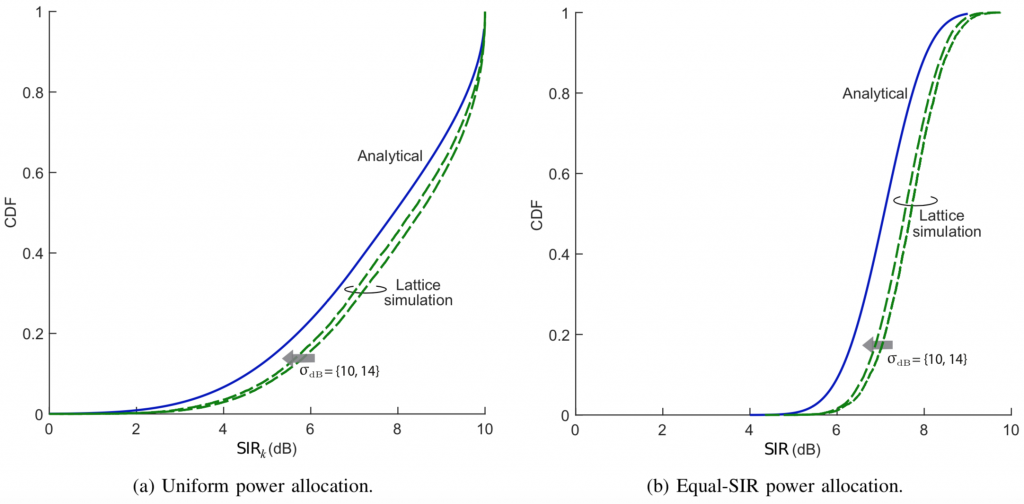
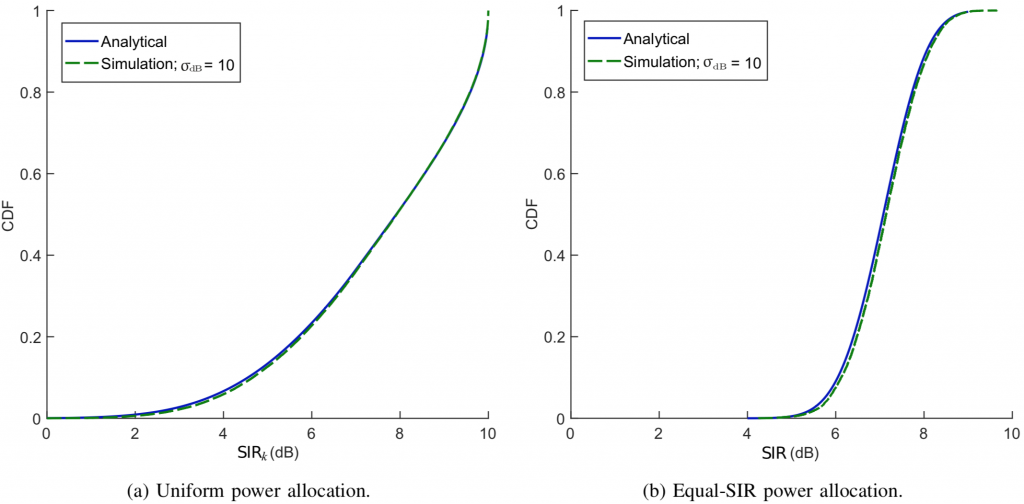
First, we simulate a 500-cell hexagonal lattice with ![]() ,
, ![]() and
and ![]() . Figs. 1a-1b compare the simulations for
. Figs. 1a-1b compare the simulations for ![]() –
–![]() dB with the analysis. The behaviors with these typical outdoor values of
dB with the analysis. The behaviors with these typical outdoor values of ![]() are well represented by the analysis and, as it turns out, in rigidly homogeneous networks such as this one is where the gap is largest.
are well represented by the analysis and, as it turns out, in rigidly homogeneous networks such as this one is where the gap is largest.
For a more irregular deployment, let us next consider a network whose BSs are uniformly distributed. BSs (500 on average) are dropped around a central one of interest. For each network snapshot, users are then uniformly dropped until ![]() of them are served by the central BS. As before,
of them are served by the central BS. As before, ![]() ,
, ![]() and
and ![]() . Figs. 2a-2b compare the simulations for
. Figs. 2a-2b compare the simulations for ![]() dB with the analysis, and the agreement is now complete. The simulated average spectral efficiency with a uniform power allocation is
dB with the analysis, and the agreement is now complete. The simulated average spectral efficiency with a uniform power allocation is ![]() b/s/Hz/user while (2) gives
b/s/Hz/user while (2) gives ![]() b/s/Hz/user.
b/s/Hz/user.
The analysis presented in this post is not without limitations, chiefly the absence of noise and pilot contamination. However, as argued in [1], there is a broad operating range (![]() –
–![]() with very conservative premises) where these effects are rather minor, and the analysis is hence applicable.
with very conservative premises) where these effects are rather minor, and the analysis is hence applicable.
[1] G. George, A. Lozano, M. Haenggi, “Massive MIMO forward link analysis for cellular networks,” arXiv:1811.00110, 2018.
[2] T. Marzetta, E. Larsson, H. Yang, and H. Ngo, Fundamentals of Massive MIMO. Cambridge University Press, 2016.
[3] H. Yang and T. L. Marzetta, “A macro cellular wireless network with uniformly high user throughputs,” IEEE Veh. Techn. Conf. (VTC’14), Sep. 2014.