One of the main impairments in wireless communications is small-scale channel fading. This refers to random fluctuations in the channel gain, which are caused by microscopic changes in the propagation environments. The fluctuations make the channel unreliable, since occasionally the channel gain is very small and the transmitted data is then received in error.
The diversity achieved by sending a signal over multiple channels with independent realizations is key to combating small-scale fading. Spatial diversity is particularly attractive, since it can be obtained by simply having multiple antennas at the transmitter or the receiver. Suppose the probability of a bad channel gain realization is p. If we have M antennas with independent channel gains, then the risk that all of them are bad is pM. For example, with p=0.1, there is a 10% risk of getting a bad channel in a single-antenna system and a 0.000001% risk in an 8-antenna system. This shows that just a few antennas can be sufficient to greatly improve reliability.
In Massive MIMO systems, with a “massive” number of antennas at the base station, the spatial diversity also leads to something called “channel hardening”. This terminology was used already in a paper from 2004:
M. Hochwald, T. L. Marzetta, and V. Tarokh, “Multiple-antenna channel hardening and its implications for rate feedback and scheduling,” IEEE Transactions on Information Theory, vol. 50, no. 9, pp. 1893–1909, 2004.
In short, channel hardening means that a fading channel behaves as if it was a non-fading channel. The randomness is still there but its impact on the communication is negligible. In the 2004 paper, the hardening is measured by dividing the instantaneous supported data rate with the fading-averaged data rate. If the relative fluctuations are small, then the channel has hardened.
Since Massive MIMO systems contain random interference, it is usually the hardening of the channel that the desired signal propagates over that is studied. If the channel is described by a random M-dimensional vector h, then the ratio ||h||2/E{||h||2} between the instantaneous channel gain and its average is considered. If the fluctuations of the ratio are small, then there is channel hardening. With an independent Rayleigh fading channel, the variance of the ratio reduces with the number of antennas as 1/M. The intuition is that the channel fluctuations average out over the antennas. A detailed analysis is available in a recent paper.
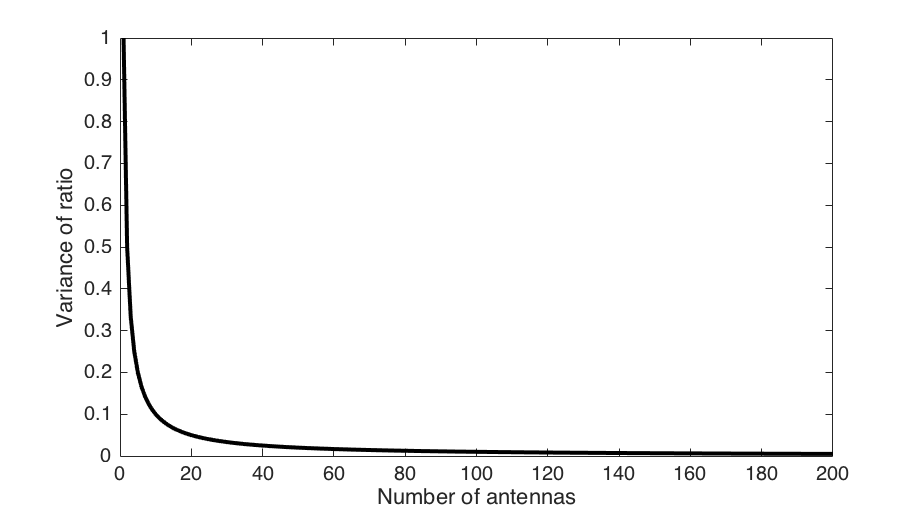
The figure above shows how the variance of ||h||2/E{||h||2} decays with the number of antennas. The convergence towards zero is gradual and so is the channel hardening effect. I personally think that you need at least M=50 to truly benefit from channel hardening.
Channel hardening has several practical implications. One is the improved reliability of having a nearly deterministic channel, which results in lower latency. Another is the lack of scheduling diversity; that is, one cannot schedule users when their ||h||2 are unusually large, since the fluctuations are small. There is also little to gain from estimating the current realization of ||h||2, since it is relatively close to its average value. This can alleviate the need for downlink pilots in Massive MIMO.

I used the MMSE estimator on a Massive MIMO channel. I noted that channel hardening of massive MIMO reduces the fluctuations of the output, but the error mean remains as Single antenna. Is that true?
Does the channel hardening of massive MIMO improves the error mean of MMSE estimator?
What you observe is correct for independent Rayleigh fading channels. The channel to each BS antenna is estimated independently when there is no correlation between the channels, thus the MSE is not affected by the number of antennas.
If you would instead consider correlated Rayleigh fading, then the MSE per antenna will reduce as you add more antennas.
Hi,
I had the same observation during my MS research as well. I simulated a massive MIMO system with linear receiver in presence of an LMMSE estimator assuming i.i.d Rayleigh fading channels. What I observed was significantly high MSE with floor. The floor elevated with increase in the number of cells which is obviously due to increase in resulted pilot contamination. Despite this undesirable MSE, the linear receiver represented very good BER behavior thanks to the large M. I repeated the simulation with small M and observed that the BER curve encountered error floor. What I realized from these results was that despite the undesirable MSE behavior of LMMSE estimation, linear receiver still can operate efficiently under asymptotically favorable propagation condition due to large number of antennas. in other words, massive MIMO brings robustness. You can take advantage of linearity of estimator and receiver while guaranteeing robustness of the overall system.
Very interesting article, thanks for sharing.
While reading the piece, I was wondering whether there are any requirements on the spacing of the antenna array elements wrt the carrier wave length? Being too close could mean higher correlation which would then break the assumption behind the probability calculation you made.
I assumed uncorrelated channel coefficients to get a simple description of the channel hardening concept. For correlated fading, one can still analyze the variance of ||h||^2/E{||h||^2} and see how close to zero it is.
Correlated channels harden more slowly, due to the eigenvalue variations in the covariance matrix. But if the two conditions in Assumption 1 in https://arxiv.org/pdf/1705.00538.pdf hold, we will get asymptotic channel hardening anyway.
In practice, I think you will have a finite-sized area where you can deploy antenna. I would then deploy as many antennas as I can with half-wavelength spacing. Adjacent antennas will have correlated channel coefficients, but it is better to have these antennas than to deploy fewer antennas with a larger antenna spacing.
* As I understand, channel hardening and favorable propagation channel are different things. Is it correct?
* Another question is: with an uncorrelated Rayleigh fading channel matrix H (MxK) (with variance 1): transpose(H)*H/M = Identity matrix (KxK) if M goes to infinity. Does it means this channel is both favorable and hardens?
* I have seen in a lot of massive MIMO paper, they claim that transpose(H)*H/M = Identity matrix (KxK) if M goes to infinity and M>>K. But why do we need M>>K, because I saw in the paper “Energy and spectral efficiency of very large multiuser MIMO system”, they claim that a very large M is enough to get: transpose(H)*H/M = Identity matrix (KxK).
* Yes.
* Yes, if you with “transpose” mean the “conjugate transpose” (also known as “Hermitian transpose”). The fact that the diagonal elements converge to deterministic constants proves the channel hardening. The fact that the off-diagonal elements converges to zero proves the favorable propagation.
* The proof is based on that M->infinity and K is constant. A consequence from this is that M>>K (infinity is much larger than any constant…).
Does this imply that if we have LoS link only (deterministic channel), massive MIMO is bound to work?
Yes, Massive MIMO works well in both LoS and non-LoS.
I have another question regarding the noise power to calculate SNR of massive MIMO in LoS conditions.
Most current works on Massive MIMO I have come across model noise as a complex gaussian random variable with 0 mean and unit variance (in linear scale).
My question is why is noise power considered to be 1 in most works?
The SNR can be expressed as SNR = p*b/sigma^2, where p is the transmit power, b is the pathloss coefficient, and sigma^2 is the noise power. The noise power is not 1, but can be computed based on the thermal noise power level.
As you say, it is common that people normalize the noise power to 1 to reduce the amount notation i their papers. This means that you include the noise variance in the transmit power term or pathloss coefficient instead. For example, one can define the SNR as p*c/1=p*c, where c=b/sigma^2 is the normalized pathloss coefficient, and 1 is the normalized noise variance.
Hi Emil,
My first question is: Massive MIMO can be MU-MIMO at the same time, no? I haven’t yet go through your post with the topic “Six Differences Between MU-MIMO and Massive MIMO”.
My second question is: for MU-MIMO, with LOS scenario, we cannot serve more than one user simultaneously, no?
1. As you can read in the blog post “Six Differences Between MU-MIMO and Massive MIMO”, Massive MIMO is not only multi-user MIMO with many antennas, but there other important design considerations.
2. We can serve many users in LOS scenarios, as long as the users are located in different angular directions. Chapter 1 in my book Massive MIMO networks is exemplifying this further.
I have a small doubt. What is the exact meaning of channel after beamforming? How many steering vectors are there, is it the number of terminals? Each pair is constant or over all it is same for all terminals?
The terminology “channel after beamforming” was not used in this blog post, but it usually refers to the scalar channel that you get by taking the inner product between the channel vector and the beamforming vector.
When we talk about channel hardening, we are only considering one user channel and the beamforming selected to communicate over that channel.
The interfering channels will typically not harden.
Thank you for the clarification. I have another question about beamforming vector dimension. For each terminal, I have to assign a beamforming vector for each terminal or only one beamforming vector across all terminals. May I expect any kind of power gain or power control benefit by modelling channel?
Each terminal is assigned an individual beamforming vector that is tailored to its channel, which can be viewed as directing a beam towards that terminal. The base station sends a superposition of the beamformed signals.
The better you know the channel vector to a terminal, the better you can direct a beam towards that terminal. This leads to a power gain. The more antennas you have, the more directive the beams is, which also leads to a power gain.
For the non-fading case, the channel may no longer be stationary (do not converge to mean value of signal power) and MPCs experience only path-loss or shadowing effects i.e., slow fading case. Since the channel looses stationarity can we say that massive MIMO needs more frequent feedback information?
If there is no fading, the channel is deterministic from the beginning and there is no need for channel hardening.
When you talk about stationarity, I think what you refer to are users that move around. The hardening only applies to small-scale fading effects and not variations in the large-scale fading effects (path-loss, shadowing).
I have seen papers on massive MIMO in line-of-sight conditions concluding that massive MIMO works well in line-of-sight too. However, most of them assume perfect channel estimation. Does massive MIMO work in line of sight with imperfect channel state information as well?
If we talk about mm-wave Massive MIMO, where paths are mostly line-of-sight and assume that channel will be estimated by uplink pilots only (TDD mode and reciprocity), will Massive MIMO work in such conditions too?
Yes! You will lose a bit in performance due to the imperfect channel estimation, but nothing fundamentally different will happen.
According to my understanding, in small cells mm-wave massive MIMO, since channels are mostly deterministic line-of-sight from the beginning, the channels can be thought of as already ‘hardened’ without the need for large M. The variance of ||h||^2/E[||h||^2] is almost 0 even with small number of BS antennas.
However, it seems that favourable propagation condition might not be met in this case. (h^H)*(h)/M would not go to 0 as M goes to infinity.
So what would be the implications on sum throughput/capacity of such systems where the channel hardening condition is already satisfied but favourable propagation condition is not met?
I read the paper, “No downlink pilots are needed in TDD Massive MIMO” and it explains what would happen in keyhole channels (without favourable propagation and without channel hardening), but I want to know what would happen in systems without favourable propagation but with channels already “hardened”?
I am asking this question in context of low mobility users since for high mobility users, it might be a different story.
In the absence of favorable propagation, it might be better to serve one user at a time (OFDMA/FDMA/TDMA) than to spatially multiplex them.
Thanks for sharing this interesting topic. I have a question about the nearly deterministic channel, does it mean deterministic on time domain or frequency domain? In another word, is frequency selectivity or time variation that can be ignored by channel hardening?
These are good questions that I receive quite often. I therefore decided to reply to you by writing a new blog post:
http://ma-mimo.ellintech.se/2018/04/23/estimating-channels-under-channel-hardening/
What happens if antennas are not co-located (i.e. distributed massive MIMO) and each of them has different large-scale fading coefficients? Does channel hardening still apply?
There will be some hardening, but much less than with co-located arrays. This is something that we analyzed in the following paper:
Zheng Chen, Emil Björnson, “Channel Hardening and Favorable Propagation in Cell-Free Massive MIMO with Stochastic Geometry,” IEEE Transactions on Communications, To appear. (https://arxiv.org/pdf/1710.00395)
Hello, Dr. Bjornson.
Can we say that the channel hardening is caused because the phases of the received signal in the antenna array become the same when the number of the antennas become infinity?
Another question is that whether the space between adjacent antenna affect channel hardening?
First question: No, rather that we obtain many independent random realizations and therefore the variations average out (see the law of large numbers).
Second question: Yes, the antennas should observe channel realizations that are as uncorrelated as possible. Large antenna spacing leads to less correlation.
I have one question
For extremely large aperture array since it is part of massive MIMO
can we consider that we have channel hardening for this array scheme?
Yes, that is likely to be the case, but it always depends on the channel model. If you have a correlated Rayleigh fading model, then you can use methods from Section 2 in my book Massive MIMO Networks to evaluate the channel hardening. In principle, ELAA is a Massive MIMO system with many antennas and dense arrays.
In massive MIMO, we don’t always get channel hardening (CH) and favorable propagation (FP). In Rician fading channel, we see few eigen values of equivalent channel matrix which are not uniformly spread whereas almost all the eigen values are spread uniformly. Does it mean that CH or FP fails only in Rician fading massive MIMO.
I mean eigen values are spread uniformly in Rayleigh fading channel.
The main property of channel hardening is that the effective channel becomes (almost) deterministic, despite the existence of multipath fading. Since the LOS path is deterministic (at least its magnitude), then a Rician fading channel will be less random than a Rayleigh fading channel. You will still get channel hardening, but you start from a better situation.
Favorable propagation also appears with Rician fading. I recommend you to read Sections 7.2.2-3 in Fundamentals of Massive MIMO. It covers favorable propagation with LOS paths.
https://arxiv.org/pdf/1805.07972.pdf
Thanks Dr. Emil Björnson .
I mean for LOS path, there is a small non-zero probability where favorable propagation fails.
I have one more question.
In cell free massive MIMO system, we get one good advantage of having full rank channel matrix even for LOS propagation due to multiple streams from each access points (APs). This is something which is unlikely in cellular massive MIMO system where we get rank deficient channel matrix (due to only one propagation direction). Does this mean we get channel hardening even for a LOS in cell free massive MIMO.
I mean for LOS path, there is a small non-zero probability where favorable propagation fails.
It depends on how you define favorable propagation. For a given number of antennas, you will have a fixed beamwidth and there is a risk that two users fall into it, so that you cannot cancel interference effectively. However, for two closely spaced users, as you increase the number of antennas, the beamwidth will shrink and eventually the channel vectors become orthogonal. So you will get favorable propagation also in LOS cases.
Does this mean we get channel hardening even for a LOS in cell free massive MIMO.
If you have a LOS-dominant channel, the fading variations will be small (relatively speaking) so you don’t need any extra hardening. In the extreme case of free-space LOS (no fading), the channel gain is deterministic so you don’t need any hardening. Will the (small) fading variations average out as the number of antennas increase? Yes, if you consider a fixed number of access points that each has more and more antennas. No, if you consider that you add more and more access points (it will depend on how the new access points are added, see https://arxiv.org/pdf/1710.00395.pdf).
Hi Emil,
you mentionned that “There is also little to gain from estimating the current realization of ||h||2, since it is relatively close to its average value. This can alleviate the need for downlink pilots in Massive MIMO.”
Why did you mention about downlink pilots only?
The base station needs to know the complete channel vector to perform receive combining and transmit precoding. This information is estimated based on uplink pilots. The user device needs know precoded channel ||h||^2. If it is nearly deterministic, there is no need to estimate it (or sending downlink pilots to enable it). Here is another blog post that elaborate more on this: https://ma-mimo.ellintech.se/2018/11/02/when-are-downlink-pilots-needed/