We are used to measuring performance in terms of the signal-to-interference-and-noise ratio (SINR), but this is seldom the actual performance metric in communication systems. In practice, we might be interested in a function of the SINR, such as the data rate (a.k.a. spectral efficiency), bit-error-rate, or mean-squared error in the data detection. When the receiver has perfect channel state information (CSI), the aforementioned metrics are all functions of the same SINR expression, where the power of the received signal is divided by the power of the interference plus noise. Details can be found in Examples 1.6-1.8 of the book Optimal Resource Allocation in Coordinated Multi-Cell Systems.
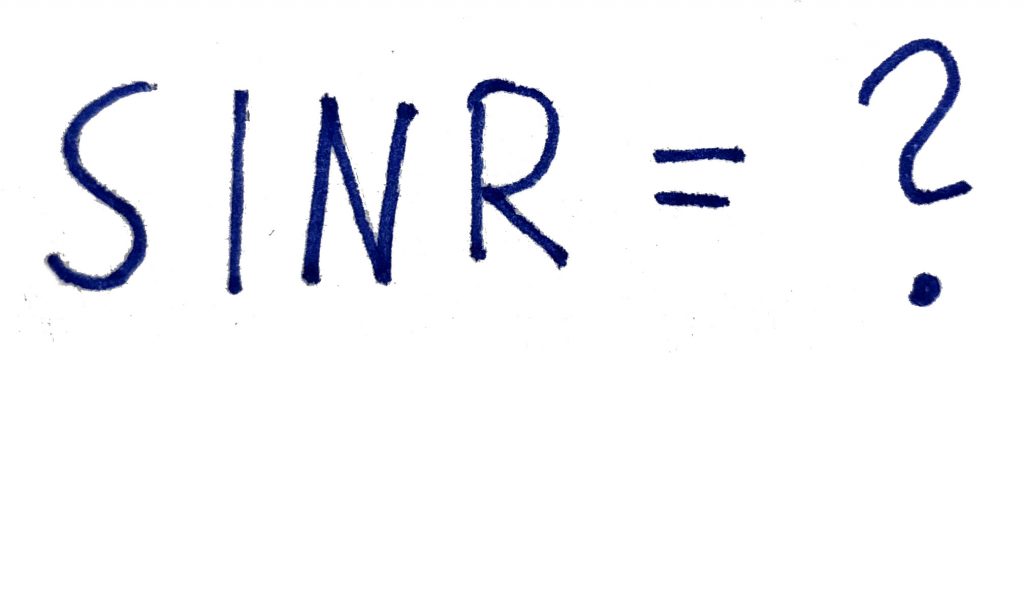 In most cases, the receiver only has imperfect CSI and then it is harder to measure the performance. In fact, it took me years to understand this properly. To explain the complications, consider the uplink of a single-cell Massive MIMO system with
In most cases, the receiver only has imperfect CSI and then it is harder to measure the performance. In fact, it took me years to understand this properly. To explain the complications, consider the uplink of a single-cell Massive MIMO system with ![]() single-antenna users and
single-antenna users and ![]() antennas at the base station. The received
antennas at the base station. The received ![]() -dimensional signal is
-dimensional signal is
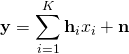
where ![]() is the unit-power information signal from user
is the unit-power information signal from user ![]() ,
, ![]() is the fading channel from this user, and
is the fading channel from this user, and ![]() is unit-power additive Gaussian noise. In general, the base station will only have access to an imperfect estimate
is unit-power additive Gaussian noise. In general, the base station will only have access to an imperfect estimate ![]() of
of ![]() , for
, for ![]()
Suppose the base station uses ![]() to select a receive combining vector
to select a receive combining vector ![]() for user
for user ![]() . The base station then multiplies it with
. The base station then multiplies it with ![]() to form a scalar that is supposed to resemble the information signal
to form a scalar that is supposed to resemble the information signal ![]() :
:
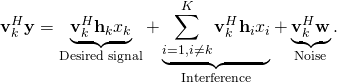
From this expression, a common mistake is to directly say that the SINR is
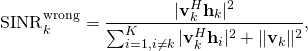
which is obtained by computing the power of each of the terms (averaged over the signal and noise), and then claim that ![]() is an achievable rate (where the expectation is with respect to the random channels). You can find this type of arguments in many papers, without proof of the information-theoretic achievability of this rate value. Clearly,
is an achievable rate (where the expectation is with respect to the random channels). You can find this type of arguments in many papers, without proof of the information-theoretic achievability of this rate value. Clearly, ![]() is an SINR, in the sense that the numerator contains the total signal power and the denominator contains the interference power plus noise power. However, this doesn’t mean that you can plug
is an SINR, in the sense that the numerator contains the total signal power and the denominator contains the interference power plus noise power. However, this doesn’t mean that you can plug ![]() into “Shannon’s capacity formula” and get something sensible. This will only yield a correct result when the receiver has perfect CSI.
into “Shannon’s capacity formula” and get something sensible. This will only yield a correct result when the receiver has perfect CSI.
A basic (but non-conclusive) test of the correctness of a rate expression is to check that the receiver can compute the expression based on its available information (i.e., estimates of random variables and deterministic quantities). Any expression containing ![]() fails this basic test since you need to know the exact channel realizations
fails this basic test since you need to know the exact channel realizations ![]() to compute it, although the receiver only has access to the estimates.
to compute it, although the receiver only has access to the estimates.
What is the right approach?
Remember that the SINR is not important by itself, but we should start from the performance metric of interest and then we might eventually interpret a part of the expression as an effective SINR. In Massive MIMO, we are usually interested in the ergodic capacity. Since the exact capacity is unknown, we look for rigorous lower bounds on the capacity. There are several bounding techniques to choose between, whereof I will describe the two most common ones.
The first lower bound on the uplink capacity can be applied when the channels are Gaussian distributed and ![]() are the MMSE estimates with the corresponding estimation error covariance matrices
are the MMSE estimates with the corresponding estimation error covariance matrices ![]() . The ergodic capacity of user
. The ergodic capacity of user ![]() is then lower bounded by
is then lower bounded by
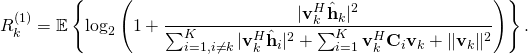
Note that this expression can be computed at the receiver using only the available channel estimates (and deterministic quantities). The ratio inside the logarithm can be interpreted as an effective SINR, in the sense that the rate is equivalent to that of a fading channel where the receiver has perfect CSI and an SNR equal to this effective SINR. A key difference from ![]() is that only the part of the desired signal that is received along the estimated channel appears in the numerator of the SINR, while the rest of the desired signal appears as
is that only the part of the desired signal that is received along the estimated channel appears in the numerator of the SINR, while the rest of the desired signal appears as ![]() in the denominator. This is the price to pay for having imperfect CSI at the receiver, according to this capacity bound, which has been used by Hoydis et al. and Ngo et al., among others.
in the denominator. This is the price to pay for having imperfect CSI at the receiver, according to this capacity bound, which has been used by Hoydis et al. and Ngo et al., among others.
The second lower bound on the uplink capacity is
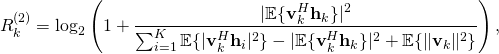
which can be applied for any channel fading distribution. This bound provides a value close to ![]() when there is substantial channel hardening in the system, while
when there is substantial channel hardening in the system, while ![]() will greatly underestimate the capacity when
will greatly underestimate the capacity when ![]() varies a lot between channel realizations. The reason is that to obtain this bound, the receiver detects the signal as if it is received over a non-fading channel with gain
varies a lot between channel realizations. The reason is that to obtain this bound, the receiver detects the signal as if it is received over a non-fading channel with gain ![]() (which is deterministic and thus known in theory, and easy to measure in practice), but there are no approximations involved so
(which is deterministic and thus known in theory, and easy to measure in practice), but there are no approximations involved so ![]() is always a valid bound.
is always a valid bound.
Since all the terms in ![]() are deterministic, the receiver can clearly compute it using its available information. The main merit of
are deterministic, the receiver can clearly compute it using its available information. The main merit of ![]() is that the expectations in the numerator and denominator can sometimes be computed in closed form; for example, when using maximum-ratio and zero-forcing combining with i.i.d. Rayleigh fading channels or maximum-ratio combining with correlated Rayleigh fading. Two early works that used this bound are by Marzetta and by Jose et al..
is that the expectations in the numerator and denominator can sometimes be computed in closed form; for example, when using maximum-ratio and zero-forcing combining with i.i.d. Rayleigh fading channels or maximum-ratio combining with correlated Rayleigh fading. Two early works that used this bound are by Marzetta and by Jose et al..
The two uplink rate expressions can be proved using capacity bounding techniques that have been floating around in the literature for more than a decade; the main principle for computing capacity bounds for the case when the receiver has imperfect CSI is found in a paper by Medard from 2000. The first concise description of both bounds (including all the necessary conditions for using them) is found in Fundamentals of Massive MIMO. The expressions that are presented above can be found in Section 4 of the new book Massive MIMO Networks. In these two books, you can also find the right ways to compute rigorous lower bounds on the downlink capacity in Massive MIMO.
In conclusion, to avoid mistakes, always start with rigorously computing the performance metric of interest. If you are interested in the ergodic capacity, then you start from one of the canonical capacity bounds in the above-mentioned books and verify that all the required conditions are satisfied. Then you may interpret part of the expression as an SINR.

I just want to add another kind of problem, which I see in the SINR analysis for the downlink channels (I hope I’m not wrong).
The paper “MMSE transmit optimization for multi-user multi-antenna systems” explains how one can derive the MMSE transmit filters for the downlink channel for the perfect CSI.
This paper emphasizes the importance of the scaling factor that each user is using to estimate its symbols (beta_i). However, in the SINR analysis, this can not be taken into account (since it is only a scaling factor at the receiver, which is cancelled when you derive the SINR formula for that user). However, this is important for the user to correctly estimate its symbols.
So, I guess, when we are talking about SINR formulas, we implicitly assume that each receiver is using the correct scaling factor to estimate its symbol. Otherwise, in practice, the user can not achieve the data rate, guaranteed by the SINR value.
Thus, I think it’s better to use the normalized MSE or bit error rate for the downlink to avoid this ambiguity, rather than the data rates derived with the SINR values.
Your observation is correct. When computing the mutual information between the input and output of a channel, it is implicitly assumed that the receiver is doing the optimal type of reception, given the information that is available on the receiver side. This implicit assumption carries over to SINRs that are obtained from the mutual information expressions.
However, I don’t see this as a problem. If a practical receiver cannot compute the optimal scaling factors that you refer to, then we have computed the mutual information in the wrong way; apparently, the received didn’t have access to all the information that we assumed it to have.
That said, I also think that the MSE or bit error rate can be good performance measures, but only for transmission of small packets, where one cannot operate at a rate close to the mutual information using a practical channel code. (See Fig. 3 in “Massive MIMO: Ten Myths and One Critical Question” for some details on that).
Very thanks for the explanation.
Thank you for the nice post. Could you please give some explanation regarding the uncorrelation (independence) assumptions between the different terms in Eq. 2 above. Is there a required uncorrelation/independence between the second and third terms to be a valid SINR? Also between the desired signal, interference signal, and noise signal? Thanks!
This is an important question. One should never look at a received signal and try to guess what a valid SINR should be. Instead, one should start from a well-established capacity lower bound and apply it to the received signal. These bounds often result in something of the type log2(1+SINR) or E{log2(1+SINR)}, but the “SINR” looks different depending on how the first, second, and third term are correlated (or uncorrelated) and also what kind of channel state information that the receiver has.
You can have a look at Corollary 1.3 in my book https://www.nowpublishers.com/article/DownloadSummary/SIG-093
and try to figure out what h, v, and n will be in your case. Then you need to verify that the necessary conditions stated in the corollary are satisfied so that it can be applied. If not, you need to revise what you call h, v, and n.
Alternatively, you can read Section 2.3 in Fundamentals of Massive MIMO and use one of the bounds that are listed there.
Hi,
As I understand, to compute R_k^1, we need also know the distribution of channel estimation (error distribution). The expectation is now taken with respect to the estimated channel I guess. If we only know the channel estimates we still may not be able to compute R_k^1, it seems.
That is correct. But you can only compute the estimates if you know the statistics, so it is natural that you know the error statistics as well.
This is a an excellent observation for sure. But in practical wireless systems, almost all wirless standards have enured that channel training, via pilot tones or signals, could yield channel estimates with very low MSE.
In other words, using SINR would serve engineers with very little loss of precision to compute a bound on data rate in the Shannon sense, except in few cases, while it may not be the case in the academic world.
Yes, in a cellular network, you will get very accurate channel estimates in the cell center but not necessarily at the cell edge. This is particularly challenging in reciprocity-based Massive MIMO where you estimate the channels using uplink pilots. Channel estimates made in the uplink are more resource efficient since you can estimate the channel to any number of antennas from just a single pilot tone, but the SNR might be 20 dB worse than in the downlink. This is a real problem experienced in the industry.
Another motivation behind this blog post is that even if you can get a good estimate of the desired signal’s channel, the SINR also contain interfering signals. It is not realistic to believe that one can estimate all of them with high accuracy.
Does high SINR of a received signal necessarily mean high data rate? Is this possible that SINR of a received signal is low but the data rate or the capacity achieved is higher than the channel with high SINR?
No, the data rate is (approximately) log2(1+SINR), thus it is proportional to the SINR.
Can I treat the effective SINR in R^(2) as an instantaneous SINR given the several expectations are obtained at the base station? Thank you.
I have sometimes called it an “instantaneous effective SINR”, but it is not measurable at any point in time. The effective SINR contains the instantaneous channel estimate but averaging over the estimation errors.
Can you recommend a source in literature dealing with the case of imperfect CSI in TDD SINR analysis for the case of both favourable and non favourable propagation conditions ?
Thanks
I’m not sure I understand what you are looking for. Imperfect CSI and favorable propagation are two unrelated things.
But my book “Massive MIMO networks” deals with imperfect CSI with arbitrary spatial correlation matrices. Depending on how you select the correlation matrices, you will or will not get favorable propagation.
Hi Prof. Emil, can we see the log(1+SINR^{Wrong}) as an upper bound to the maximum achievable rate?
Yes, I think so. But an upper bound on a rate, which is by itself a lower bound on the capacity, what is that? It is more like an approximation.
Why in so many papers for channel estimation or signal detection, the performance parameter SNR instead of SINR?
SNR range is considered over 0 to 20 dB, why is SINR not considered to plot a graph?
May this is a silly question, but I am confused here.
When running a simulation, you need to select which parameters are given as input and which are computed as part of the simulation.
People often let the SNR be an input parameter, which is then plotted on the horizontal axis, and then they plot the resulting output performance on the vertical axis. The performances could be the MSE in channel estimation or MSE/SINR/BER/rate for data transmission.
Hello Prof,
In the equation for SINR_k^{wrong}, why we are not considering the small scale channels?
h_k and h_i are the instantaneous channel vectors in this equation, which include small-scale fading, so that phenomenon is taken into account. The expectation mentioned in the paragraph after the equation is computed with respect to the small-scale fading. However, the equation is wrong for other reasons…
Hello Prof,
I have a doubt with respect to the SIR and SINR relations I came across in a paper. In the system model, there is one desired transmitter-receiver pair and many interfering transmitters. In the SINR relation, channel coefficients h_k are considered in the numerator and denominator, whereas in the SIR relation, the channel coefficients are not considered in the numerator and denominator. Is it because of the channel coefficients are encapsulated within the path loss terms d^-{\alpha}, where d is the distance between the transmitter and receiver and \alpha is the path loss exponent.
In general, one should get the SIR expression by removing the noise term from the SINR expression.
If the paper contains a different expression, it may be as you are saying: The authors assume a specific (simplistic) pathloss model and use it to rewrite the SIR expression.
If you give me the name of the paper, I can have a look at the expressions and evaluate if they seem to be correct.
I have mentioned the papers below.
In [1], the SINR relations where channel coefficients are considered are given in (2a) and (2b), whereas the SIR relations where channel coefficients are not considered are given in (3) and (6).
In [2], the SINR relations where channel coefficients are considered are given in (4), (5), and (6), whereas the SIR relations where channel coefficients are not considered are given in (8) and (9).
References:
1) J. Sun, Z. Zhang, H. Xiao and C. Xing, “Uplink Interference Coordination Management With Power Control for D2D Underlaying Cellular Networks: Modeling, Algorithms, and Analysis,” in IEEE Transactions on Vehicular Technology, vol. 67, no. 9, pp. 8582-8594, Sept. 2018
Link: https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=8405600
2) X. Liu, H. Xiao and A. T. Chronopoulos, “Joint Mode Selection and Power Control for Interference Management in D2D-Enabled Heterogeneous Cellular Networks,” in IEEE Transactions on Vehicular Technology, vol. 69, no. 9, pp. 9707-9719, Sept. 2020
Link: https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9115903
I wouldn’t pay much attention to these papers. There is an elementary error in the pathloss modeling, where the papers assume d^-alpha.
Any reasonable model must also contain a constant term (the pathloss at d=1 reference distance), which is typically at the order of -50 dB. So the pathloss models are roughly five order of magnitude wrong…
Since the small-scale fading terms h~CN(0,1) have a variance of 1, the expectation of |h|^2 is equal to 1. I guess this is what they are doing when writing out the SIR terms, but it is really not clear.
These issues are unfortunately repeating in a lot of stochastic geometry papers. Researchers like to pick models that are analytically tractable when using such tools, instead of models that are practically meaningful.