Humans can estimate the distance to objects using our eyesight. This perception of depth is enabled by the fact that our two eyes are separated to get different perspectives of the world. It is easier to determine the distance from our eyes to nearby objects than to things further away, because our visual inputs are then more different. The ability to estimate distances also varies between people, depending on the quality of their eyesight and ability to process the visual inputs in their brains.

An antenna array for wireless communications also has a depth perception; for example, we showed in a recent paper that if the receiver is at a distance from the transmitter that is closer than the Fraunhofer distance divided by 10, then the received signal is significantly different from one transmitted from further away. Hence, one can take D²/(5λ) as the maximum distance of the depth perception, where D is the aperture length of the array and λ is the wavelength. The derivation of this formula is based on evaluating when the spherical curvatures of the waves arriving from different distances are significantly different.

Our eyes are separated by roughly D=6 cm and the wavelength of visual light is roughly λ=600 nm. The formula above then says that the depth perception reaches up to 1200 m. In contrast, a typical 5G base station has an aperture length of D=1 m and operates at 3 GHz (λ=10 cm), which limits the depth perception to 2 m. This is why we seldom mention depth perception in wireless communications; the classical plane-wave approximation can be used when the depth variations are indistinguishable. However, the research community is now simultaneously considering the use of physically larger antenna arrays (larger D) and the utilization of higher frequency bands (smaller λ). For an array with length D=10 m and mmWave communications at λ=10 mm, the depth perception reaches up to 2000 m. I therefore believe that depth perception will become a standard feature in 6G and beyond.

There is a series of research papers that analyze this feature, often implicitly when mentioning terms such as the radiative near-field, finite-depth beamforming, extremely large aperture arrays, and holographic MIMO. If you are interested in learning more about this topic, I recommend our new book chapter “Near-Field Beamforming and Multiplexing Using Extremely Large Aperture Arrays“, authored by Parisa Ramezani and myself. We summarize the theory for how an antenna array can transmit a “beam” towards a nearby focal point so that the focusing effect vanishes both before and after that point. This feature is illustrated in the following figure:

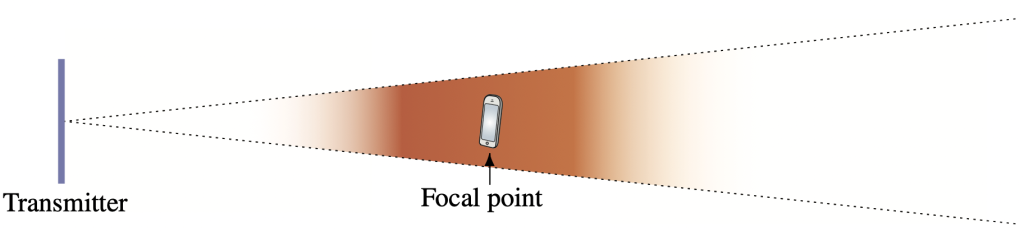
This is not a physical curiosity but enables a large antenna array to simultaneously communicate with user devices located in the same direction but at different distances. The users just need to be at sufficiently different distances so that the focusing effect illustrated above can be applied to each user and result in roughly non-overlapping focal regions. We call this near-field multiplexing in the depth domain.

A less technical overview of this emerging topic can also be found in this video:

I would like to thank my collaborators Luca Sanguinetti, Özlem Tuğfe Demir, Andrea de Jesus Torres, and Parisa Ramezani for their contributions.