A defining factor for the early Massive MIMO literature is the study of communication systems where the number of base station antennas goes to infinity. Marzetta’s original paper considered this asymptotic regime from the outset. Many other papers derived rate expressions for a finite value, and then studied their behavior as . In these papers, the signal-to-noise ratio (SNR) grows linearly with , and the rate grows towards infinity as (except when pilot contamination is a limiting factor).

I have carried out such asymptotic analysis myself, but there is one issue that has been disturbing me for a while: The SNR cannot grow without bound in practice because we can never receive more power than what was transmitted from the base station. It doesn’t matter how many transmit antennas that are used or how razor-sharp the beams become, the law of conservation of energy must be respected. So where is the error in the analysis?

The problem is not that implies the use of infinitely large arrays. If we accept that the universe is infinite, it is plausible to create an -antenna planar array for any value of , for example, using a grid. Such an array is illustrated in Figure 1.

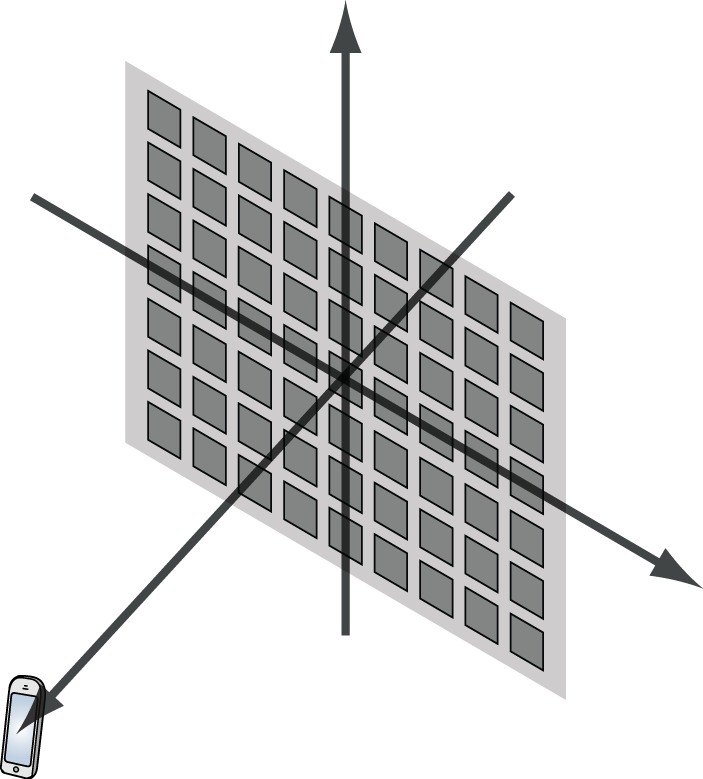
The actual issue is how the channel gains (pathlosses) between the antennas and the user are modeled. We are used to considering channel models based on far-field approximations, where the channel gain is the same for all antennas (when averaging over small-scale fading). However, as the size of the array grows, the approximate far-field models become inaccurate. Instead, one needs to model the following phenomena that appear in the near-field:

1. The propagation distance is different between each base station antenna and the user.
2. The effective antenna areas vary in the array, even if the physical areas are equal, since the antennas are observed from different angles.
3. The polarization losses vary between the antennas, because of the different angles from the antennas to the user.

It might seem complicated to take these phenomena into account, but the following paper shows how to compute the channel gain exactly when the user is centered in front of the array. I generalized this formula to non-centered users in a new paper. We utilized the new result to study the asymptotic behaviors of Massive MIMO and also intelligent reflecting surfaces. It turned out that all the three aforementioned phenomena are important to get accurate asymptotic results. When transmitting from an isotropic antenna to a planar Massive MIMO array, the total channel gain converges to 1/3 and instead of going to infinity. The remaining 2/3 of the transmit power is lost due to polarization mismatch or radiation into the opposite direction of the array. If any of the first two phenomena are ignored, the channel gain will grow unboundedly as , which is physically impossible. If the last one is ignored, the asymptotic channel gain is overestimated by 50%, so this is the least critical factor.

Although the exact channel model can be used to accurately predict the asymptotic SNR behavior, my experience from studying this topic is that the far-field approximations are accurate in most cases of practical interest. It is first when the propagation distance is shorter than the side length of the array that the near-field phenomena are critically important. In other words, the scaling laws that have been obtained in the Massive MIMO literature are usually applicable in practice, even if they break down asymptotically.