What is Massive MIMO? The term has been used for many different systems and the only common denominator seems to be a multi-user MIMO system with everything between 10 to infinitely many antennas. In the book [1], the authors give the following definition:
“Massive MIMO is a useful and scalable version of Multiuser MIMO. There are three fundamental distinctions between Massive MIMO and conventional Multiuser MIMO. First, only the base station learns G. Second, M is typically much larger than K, although this does not have to be the case. Third, simple linear signal processing is used both on the uplink and on the downlink. These features render Massive MIMO scalable with respect to the number of base station antennas, M.”
(Note: M is the number of antennas, K is the number of users, and G denotes the channel matrix).
In [2], we find another definition:
“Massive MIMO is a multi-user MIMO system with M antennas and K users per BS. The system is characterized by M ≫ K and operates in TDD mode using linear uplink and downlink processing.”
Both are nice general definitions that cover most systems that commonly are called “Massive MIMO”. However, their generality also makes them vague and they fail to pinpoint the essence of Massive MIMO. Here, is my take on a slightly more precise definition:
“Massive MIMO is a multi-user MIMO system that (1) serves multiple users through spatial multiplexing over a channel with favorable propagation in time-division duplex and (2) relies on channel reciprocity and uplink pilots to obtain channel state information.”
Now, you might ask: So what is then “favorable propagation”? We need a second definition:
“The propagation is said to be favorable when users are mutually orthogonal in some practical sense.”
Again you ask: in what practical sense? If h∈ℂᴹ is the channel vector to one user and g∈ℂᴹ the channel vector to another, the users are said to be orthogonal if hᴴg = 0. Unfortunately, this is never true in a real system. It can be practically true, however, if we say that users are practically orthogonal when hᴴg/(‖h‖‖g‖) has mean zero and a variance that is much smaller than one.
There we go: a more-or-less rigorous definition of Massive MIMO. Note that this definition does not require the number of users to be small in any sense. So, to the big question: How many antennas does a base station need to be “massive”? The answer is given for the i.i.d. Rayleigh fading channel in the following curve that shows how the users’ channels become practically orthogonal as the number of antennas is increased.
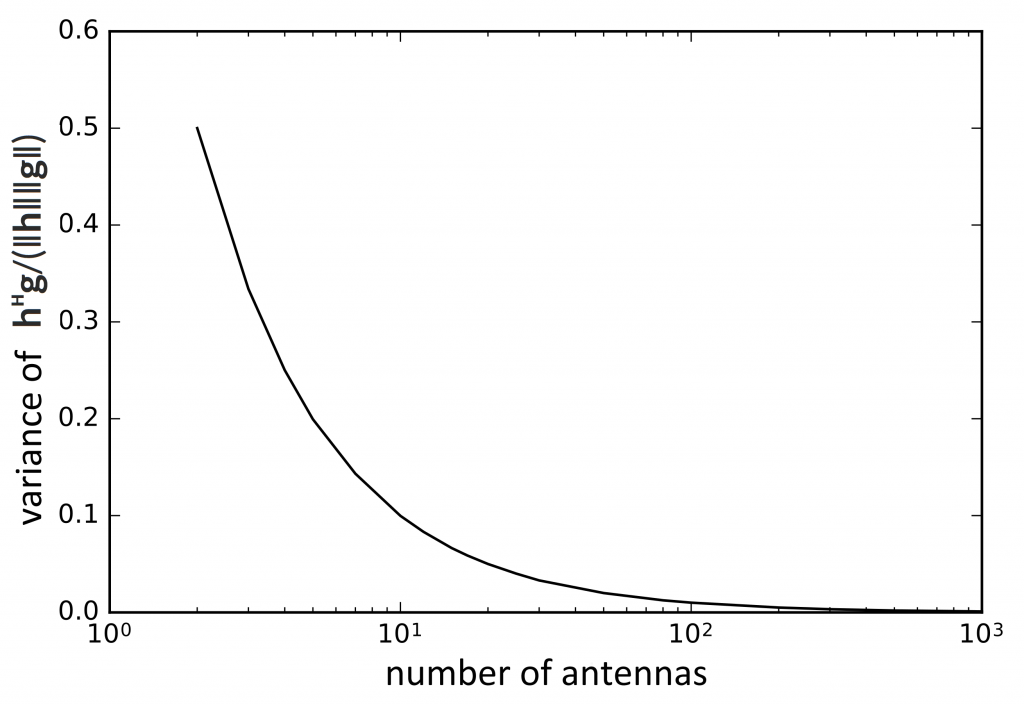
- [1] T. L. Marzetta, E. G. Larsson, H. Yang, N. Q. Ngo. Fundamentals of Massive MIMO. Cambridge University Press, 2016.
- [2] T. V. Chien, E. Björnson, “Massive MIMO Communications,” in 5G Mobile Communications, W. Xiang et al. (eds.), pp. 77-116, Springer, 2017.

Nice post! Btw, the detail of “favorable propagation” can be found in this paper:
Hien Quoc Ngo, Erik G. Larsson, and Thomas L. Marzetta, “Aspects of favorable propagation in Massive MIMO”, European Signal Processing Conference (EUSIPCO), Lisbon, Portugal, Sept. 2014.
Great contribution! Thanks for sharing this.
I think it’s worth to mention, in the definition, also the “channel hardening” property as a key benefit introduced by Massive MIMO: when the number of antennas is large (M) the channel becomes (nearly) deterministic, and hence, the effect of small-scale fading is averaged out. Hence, massive MIMO offers higher degree of channel hardening compared to multi-user MIMO.
Thanks to the channel hardening (and channel reciprocity as you said), users can reliably decode the downlink data using only long-term statistical CSI (i.e., downlink training is not needed).
How many antennas does a base station need to harden the channel? For the i.i.d. Rayleigh fading channel >50 (as well as for offering favorable propagation).
Thank you for your comment! The i.i.d. Rayleigh fading channel hardens at approximately the same rate as it becomes favourable, i.e. with >100 antennas, the channel is hard. However, it seems that not all massive MIMO channels undergo channel hardening. Think, for example, of a keyhole channel, where all propagation paths to a user depend on the single fading coefficient between the keyhole and the user. In such a channel, there might be no hardening effect, independent of the number of base station antennas. But it is still possible to serve the user with a massive MIMO base station. In such scenarios, downlink pilots might or might not be needed, because the user has to estimate the effective channel gain of the downlink. This is the topic of this paper:
Ngo, Hien Quoc, and Erik G. Larsson. “No downlink pilots are needed in TDD massive MIMO.” arXiv preprint arXiv:1606.02348 (2016).
I agree with you. The channel hardening property does not depend exclusively on the number of antennas, but also on the channel model. Thank you for pointing that out.
I think it is still a further fundamental distinction between Massive MIMO and conventional multi-user MIMO which is worth to mention.
Sir,
Can i get below paper
“Ngo, Hien Quoc, and Erik G. Larsson. “No downlink pilots are needed in TDD massive MIMO.” arXiv preprint arXiv:1606.02348 (2016)”.
This paper is publicly available on arXiv.org: https://arxiv.org/pdf/1606.02348
What is a keyhole channel? Why is channel hardening not achieved for keyhole channels even if more antennas are used at base station?
This is described in the following paper: https://arxiv.org/pdf/1606.02348.pdf
Dear Dr. Emil Björnson:
Recently, there are lots of works on massive MIMO relay system, but some scholars think that massive MIMO at relay node is not realistic, as relay is generally the auxiliary node for communication and could be of big size. What do you think of the massive MIMO relay topic.
The sincerity anticipates your reply.
This is a good question!
A relay with a large number of antennas will be substantially larger than a single-antenna relay/repeater, but it also has a much greater potential of spatial multiplexing.
One relevant scenario is when a macro base station acts as a relay. In this scenario, massive MIMO relaying is a contender with device-to-device (D2D) communication. If you have many single-antenna devices within the cell that wish to communicate pairwise in D2D mode, the interference level will be high and uncoordinated. Alternatively, all D2D transmitters could transmit to the massive MIMO base station, which then relays the information to the D2D receivers. This is a topic that we might return to on this blog!
Thank you for sharing this. Just one basic question: Why in all definitions of Masive MIMO it refers to TDD mode? Does Massive MIMO operate in TDD mode only? What about FDD?
Multiuser MIMO works at its best in TDD mode, since one can estimate the channels efficiently and accurately using only pilot signals (no codebooks and no feedback are required). This is exploited in Massive MIMO to deliver the MIMO gains under realistic conditions.
Can it work also in FDD mode? That is a critical question, as explained in our article: http://arxiv.org/pdf/1503.06854
You can also read our new post “Field Tests of FDD Massive MIMO”.
Thank you for the sharing! After understanding what is massive MIMO, can anyone give a brief explanation on how Massive MIMO detection is performed and related recent papers including algorithms.
Thank you again!
A brief explanation can be found in the book chapter:
Trinh Van Chien, Emil Björnson, “Massive MIMO Communications,” in 5G Mobile Communications, W. Xiang et al. (eds.), pp. 77-116, Springer, 2017. (http://www.diva-portal.org/smash/get/diva2:1049059/FULLTEXT02.pdf)
For more detailed information, I would recommend the book “Fundamentals of Massive MIMO”.
You can also watch the video of my talk “Advanced Signal Processing for Massive MIMO”, which cover the state-of-the-art algorithms.
Could you please give me the answer to the question: Why do we need M ≫ K? I think based on the law of large numbers, the channel vector between different users become orthogonal to each other: hᴴg/M -> 0; it is favorable propagation, I do not see any thing related to the number K?
Thank you very much!
Although hᴴg/M -> 0, as M->infinity, for any practical number of antennas, the interference between the users will be non-zero.
Suppose the interference between two users is proportional to 1/M. If you have K users, the total interference will be proportional to (K-1)/M. To make the total interference small, we need M ≫ K. Otherwise, each user will exhibit a lot of interference.
That said, you are right that M ≫ K is not a strict requirement for operating Massive MIMO. In some situations you might get a higher cell throughput by serving very many users such that M ≫ K does not hold. In Myth 6 of the paper “Massive MIMO: Ten Myths and One Critical Question,” we show that the optimal ratio of M/K can be rather small.
Thank you very much for your response, Dr. Emil Björnson.
This means that we still have room for signal detection research in massive MIMO other than linear signal detection (MMSE, ZF,..) in case M and K are very large but M/K is fixed (and not too large)? I am very interested in signal detection for massive MIMO so if possible, could you please suggest some survey or good paper in the recent trend of signal detection in massive MIMO?
Thank you very much for taking your time.
Sure, there is room for non-linear detection algorithms in Massive MIMO, but you should be aware of that people have been working on both linear and non-linear detection for multi-user MIMO for decades. The linear schemes (MMSE, ZF, MRC,…) were developed long before Massive MIMO was conceived. What Massive MIMO contributed with was a new methodology for performance analysis, which included imperfect CSI, and the utilization of behaviors such as favorable propagation and channel hardening. This made multi-user MIMO more practical, but the basic detection schemes did not change much.
I recommend you to read Page 746 in “An Overview of Massive MIMO: Benefits and Challenges” (https://doi.org/10.1109/JSTSP.2014.2317671). I think it contains some useful references on non-linear detection.
You can refer to this comprehensive survey paper:
S. Yang and L. Hanzo, “Fifty Years of MIMO Detection: The Road to Large-Scale MIMOs,” IEEE Communications Surveys & Tutorials, vol. 17, no. 4, pp. 1941-1988, 4th Quarter, 2015.
Indeed, but one should keep in mind that advanced MIMO detection schemes are of main importance in systems where the number of spatially multiplexed data streams is similar to the number of receive antennas. This could be point-to-point links with many antennas at both sides. In Massive MIMO, we typically have many more antennas than data streams. As soon as you have twice as many antennas as data streams, ZF detection provides almost as good performance as the optimal detector. (See Myth 5 in https://arxiv.org/pdf/1503.06854.pdf)
Sir,
i think ” ‖h‖” is norm of channel vector and |h| is magnitude of channel vector. My questions are
1) how both are different
2) ||h|| calculated
3) ||h||, what it indicate practically or what is physical significance of it.
4) Also there are many type norm how they are differing
Hi!
The magnitude can only be computed for scalars, not for vectors.
1) The norm is an extension of the magnitude concept but for vectors.
2) Please see this page: https://en.wikipedia.org/wiki/Norm_(mathematics)#Euclidean_norm
3) It represents the gain/attenuation of the multiantenna channel, when using the optimal maximum ratio processing.
4) Yes, there are different types of norms. We consider the standard Euclidian norm, also known as L2-norm
Dear Sir
I’m novice in MIMO. I’m confused the folliowing. Could you please clarify?
1) Multiuser MIMO uses the same frequency for multiple users. V-BLAST is used to cancel interference among users. MU-MIMO does not mention channel orthogonality. Beamforming means interference cancellation both uplink and downlink.
2) Why Massive MIMO needs channel orthogonality? Can’t use V-BLAST without it?
3) Still need beamforming(Interference cancellation) if multi users use different resources?
4) MIMO beamforming is different from phased array?
Phased array controls the phase of antenna elements. There is real (physical) beamforming direction.
In case of MIMO beamforming, is it possible to control the phase of each element for every user? Beamform direction is physical or abstract?
My understanding is it is abstract. Abstract means just a cancellation (nulling) of other user, not phase control for physical direction.
Regards.
Michael
Hi Michael!
1) V-BLAST is a method for SU-MIMO systems, not MU-MIMO. Since all the “user antennas” in belong to the same device, they can all be utilized to transmitted all the layers. Hence, no channel orthogonality is needed.
2) The reason is that the user antennas belong to different devices. The devices cannot cooperate, so we want to make sure that each devices receives its desired signal with a limited amount of interference.
3) If they use different time/frequency resources, there is no interference and thus no interference cancellation is needed. But beamforming is still useful to increase the SNR for each user.
4) An analog phased array must apply the same precoding/beamforming at every subcarrier and only send one beam, which is pointing in an angular direction seen from the array. In Massive MIMO, a digital beamforming array is used to be able to change the beamforming on each subcarrier and also create multiple beams per subcarriers, which is need to carry out MU-MIMO.
Yes, the beamforming direction is abstract. There are only three dimensions in our world, but with 64 antennas, you are selecting the beamforming in a. 64-dimensional vector space. Many of them are not representing a distinct physical direction but a superposition of many directions.
I would like to ask if multi-carrier or single-carrier modulation is preferred mostly in massive MIMO systems?
Multi-carrier modulation is mainly used today, including in massive MIMO.