The user terminals in reciprocity-based Massive MIMO transmit two types of uplink signals: data and pilots (a.k.a. reference signals). A terminal can potentially transmit these signals using different power levels. In the book Fundamentals of Massive MIMO, the pilots are always sent with maximum power, while the data is sent with a user-specific power level that is optimized to deliver a certain per-user performance. In the book Massive MIMO networks, the uplink power levels are also optimized, but under another assumption: each user must assign the same power to pilots and data.
Moreover, there is a series of research papers (e.g., Ref1, Ref2, Ref3) that treat the pilot and data powers as two separate optimization variables that can be optimized with respect to some performance metric, under a constraint on the total energy budget per transmission/coherence block. This gives the flexibility to “move” power from data to pilots for users at the cell edge, to improve the channel state information that the base station acquires and thereby the array gain that it obtains when decoding the data signals received over the antennas.
In some cases, it is theoretically preferable to assign, for example, 20 dB higher power to pilots than to data. But does that make practical sense, bearing in mind that non-linear amplifiers are used and the peak-to-average-power ratio (PAPR) is then a concern? The answer depends on how the pilots and data are allocated over the time-frequency grid. In OFDM systems, which have an inherently high PAPR, it is discouraged to have large power differences between OFDM symbols (i.e., consecutive symbols in the time domain) since this will further increase the PAPR. However, it is perfectly fine to assign the power in an unequal manner over the subcarriers.
In the OFDM literature, there are two elementary ways to allocate pilots: block and comb type arrangements. These are illustrated in the figure below and some early references on the topic are Ref4, Ref5, Ref6.
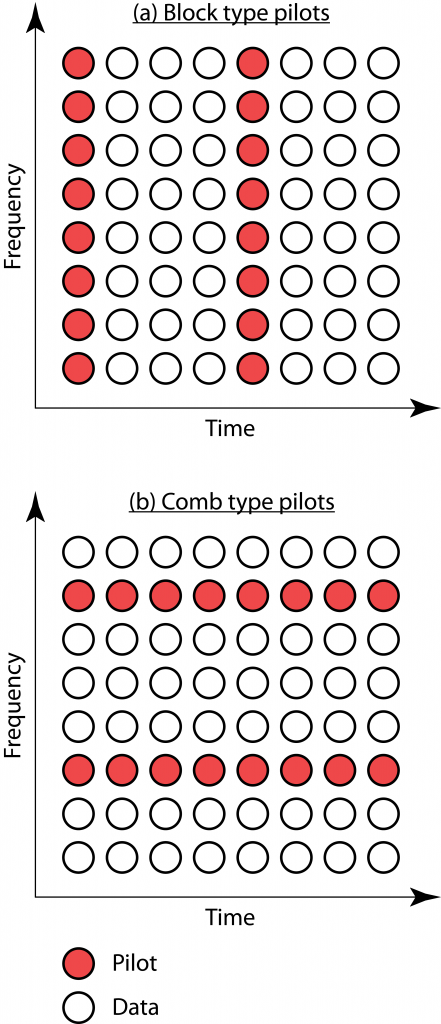
(a): In the block type arrangement, at a given OFDM symbol time, all subcarriers either contain pilots or data. It is then preferable for a user terminal to use the same transmit power for pilots and data, to not get a prohibitively high PAPR. This is consistent with the assumptions made in the book Massive MIMO networks.
(b): In the comb type arrangement, some subcarriers always contain pilots and other subcarriers always contain data. It is then possible to assign different power to pilots and data at a user terminal. The power can be moved from pilot subcarriers to data subcarriers or vice versa, without a major impact on the PAPR. This approach enables the type of unequal pilot and data power allocations considered in Fundamentals of Massive MIMO or research papers that optimize the pilot and data powers under a total energy budget per coherence block.
The downlink in LTE uses a variation of the two elementary pilot arrangements, as illustrated in (c). It is easiest described as a comb type arrangement where some pilots are omitted and replaced with data. The number of omitted pilots depend on how many antenna ports are used; the more antennas, the more similar the pilot arrangement becomes to the comb type. Hence, unequal pilot and power allocation is possible in LTE but maybe not as easy to implement as described above. 5G has a more flexible frame structure but supports the same arrangements as LTE.
In summary, uplink pilots and data can be transmitted at different power levels, and this flexibility can be utilized to improve the performance in Massive MIMO. It does, however, require that the pilots are arranged in practically suitable ways, such as the comb type arrangement.
Thanks Emil for sharing your great ideas.
I understand that in the block-type, the pilots are assigned to one full OFDM symbol (all the subcarriers at certain transmission time) with the same power of the data symbols. Whereas in the comb-type, each OFDM symbol may contain both pilot and data (allocated along the available subcarriers) with same or different power allocation. If this is true, is PAPR problem resulting in the same OFDM symbol or in OFDM frame (successive OFDM symbols)?
The time-domain signal that represents an OFDM symbol has an average power that is equal to the sum of the power assigned to the different subcarriers (the instantaneous power fluctuates around the average depending how the subcarriers are combined by FFT). If you assign different power to successive OFDM symbols, you will increase the PAPR.
Pilots are predefined sequences whose values are known to both user and BS. The BS estimates the channel gain by comparing the distorted received pilot symbols with the one it knows about, hence if any user intends for performing power control on its transmitted pilot and change the values of its pilot symbols then it must somehow feedback the BS about the new values. While pilot power control does not seem to have significant impact on MSE (since pilot power is present in both numerator and denominator of MSE equation){1}, then the only advantage remained is to avoid PAPR or reduce total power consumption. As the number of users in massive MIMO systems is huge, then huge spectral resources would be wasted on this feedback scheme. Does it worth wasting such resources for only reducing PAPR and power consumption or I’m missing some important points?
Thank you
————————————-
{1}. In “massive MIMO network” book pp.250, the effective pilot SNR and pilot processing gain is introduced. Regarding eq. 10 pp. 90 of book “5G mobile communications”, inverted effective SNR appears in the denominator of MSE equation in addition to the pilot contamination term. What I guess is that in most cases the effective pilot SNR is high and its inverse could be ignored in presence of the pilot contamination term in the denominator therefore what I understand is that changing pilot power may not have significant impact on MSE.
Each MSE a decreasing function of your own pilot power and an increasing function of all the pilot-sharing users’ pilot power. You can affect the collection of MSE values that the users are achieving a lot by adapting their pilot powers. With a smaller MSE, you will get a larger array gain in the data transmission. See the references provided in my post for quantitative examples.
As you say, the base station will typically be involved in the selection of pilot power.
I guess, spending frequency-time resources on coordinating BS with users on setting new pilot values which are optimized for lowering estimation errors might be unnecessary since the channel hardening inherently provides receiver with some degree of robustness against estimation error.
I’m not sure that I follow your argumentation. Channel hardening appears after you have estimated the channel and applied beamforming based on the estimates. The better the estimate is, the stronger the channel hardening effect will be.
My apologies for my unclear explanation.
As you mentioned, the estimation error results in poor channel hardening effect in MRC and detection error. I simulated the BER performance of receiver with MRC for few and huge number of antennas in presence of LMMSE estimation in case of i.i.d Rayleigh channels. What I observed was that when the number of antenna goes large, the BER significantly decreases even in case of very poor MSE e.g. in case of an LMMSE estimator when channels are assumed i.i.d . If my simulation result is valid then it means that even in case of poor MSE, the channel hardening appears strong enough to mitigate the interference. This question hit my mind that while implementing huge number of antennas in massive MIMO could significantly reduce the BER without being in need of improving the MSE, then maybe it is unnecessary to incorporate the pilot adaptation schemes in massive MIMO case regarding its resultant system overhead for informing BS with the pilot values through dedicated control channels which is a price to be paid in return of improving the MSE. Pilot adaptation might become even unreasonable in massive MIMO since the number of users is huge and the resulted system overhead might become severe and degrade the overall system performance. The question is: “DOES PILOT ADAPTATION SCHEME always RESULT IN IMPROVEMENT IN MASSIVE MIMO SYSTEM PERFORMANCE?”
In order to answer to this question, one needs to take the resulted overhead in to account in the optimization objective function. As far as I have seen, (of course, my knowledge of literature is not sufficient) papers I have reviewed do not include this overhead in their optimization objective functions which is equivalent to assuming that there exists always adequate vacant spectral resources left to be used for the control channels (the objective function is sum SE in which the reduction in users bandwidth because of the control channels is not taken in to account). It would be much more realistic to assume the available spectrum fixed and consider the required spectral resources by control channels as a portion of this fixed spectrum. This portion must be taken in to account in the objective function which might give totally different results. The results might give an upper bound on the number of users per cell for which the pilot adaptation scheme results in overall system improvements.
What you observe is the array gain: The desired signal power grows proportionally to the number of antennas, so more antennas will always reduce the BER and increase the achievable rate. The scaling goes as c*M where M is the number of antennas and c is a decreasing function of the MSE (so larger c when the MSE is low). Hence, the performance grows faster with M if you make the MSE smaller.
You are right that the overhead required to implemented the pilot power optimization should be accounted for. This is a concern if you change the power allocation often, based on the current small-scale fading realizations. If the power is instead selected only based on the channel statistics, which are fixed, we only need to optimize the system once and then we can use the solution “forever”. This is the case in the pilot power optimization problems that I referred to, so the overhead is negligible in this case.
Hi Professor Emil,
I have a question regarding a point mentioned in the blog stating that ”the more antennas, the more similar the pilot arrangement becomes to the comb type”. As far as I know, in a 4×4 LTE FDD system, the pilot arrangement known as the lattice type is adopted. In a such arragement, it is clearly observed that an important number of REs is consummed by pilot symbols.
My question is as follows: for an FDD 5G system where the number of antennas is way greater than 4, how the antennas are going to map the pilot signals over a resource grid of 84 (numerology 0 : 15 kHz) REs without affecting drastically the spectral efficiency?
If you have 32 antenna ports and you have no prior information about the channels, the downlink pilot transmission in an FDD system will have to explore all 32 dimensions in every resource block. This is likely not how it is going to be implemented. I don’t know the exact details, but if one can estimate dominant paths (e.g., their angles) in one resource block, it can be reused in other resource blocks.
But generally speaking, it is more convenient to carry out channel estimation in TDD systems where one can send one pilot per user in the uplink, instead of one pilot per antenna port in the downlink.
Thank you so much Sir for your reply.
In the literature, many researchers have handled the channel estimation in FDD based massive MIMO systems and they focused on feeding back the CSI to the BS and overlooked how the pilots were mapped on the resource grid at the BS side as it is an easy operation. Extending the LTE pilot arrangement to massive MIMO systems isn’t possible as it will consume the whole resource grid. My question is how these papers have first acquired the CSI at the UEs? Is there a method other than pilot based channel estimation to do so?
No, pilot based channel estimation is what is done and 5G supports that using what is called CSI-RS.