Channel estimation is critical in Massive MIMO. One can use the basic least-squares (LS) channel estimator to learn the multi-antenna channel from pilot signals, but if one has prior information about the channel’s properties, that can be used to improve the estimation quality. For example, if one knows the average channel gain, the linear minimum mean-squared error (LMMSE) estimator can be used, as in most of the literature on Massive MIMO.
There are many attempts to exploit further channel properties, in particularly channel sparsity is commonly assumed in the academic literature. I have recently received several questions about this topic, so I will take the opportunity to give a detailed answer. In particular, this blog post discusses temporal and spatial sparsity.
Temporal sparsity
This means that the channel’s impulse response contains one or several pulses with zeros in between. These pulses could represent different paths, in a multipath environment, which are characterized by non-overlapping time delays. This does not happen in a rich scattering environment with many diffuse scatterers having overlapping delays, but it could happen in mmWave bands where there are only a few reflected paths.
If one knows that the channel has temporal sparsity, one can utilize such knowledge in the estimator to determine when the pulses arrive and what properties (e.g., phase and amplitude) each one has. However, several hardware-related conditions need to be satisfied. Firstly, the sampling rate must be sufficiently high so that the pulses can be temporally resolved without being smeared together by aliasing. Secondly, the receiver filter has an impulse response that spreads signals out over time, and this must not remove the sparsity.
Spatial sparsity
This means that the multipath channel between the transmitter and receiver only involves paths in a limited subset of all angular directions. If these directions are known a priori, it can be utilized in the channel estimation to only estimate the properties (e.g., phase and amplitude) in those directions. One way to determine the existence of spatial sparsity is by computing a spatial correlation matrix of the channel and analyze its eigenvalues. Each eigenvalue represents the average squared amplitude in one set of angular directions, thus spatial sparsity would lead to some of the eigenvalues being zero.
Just as for temporal sparsity, it is not necessary that spatial sparsity can be utilized even if it physically exists. The antenna array must be sufficiently large (in terms of aperture and number of antennas) to differentiate between directions with signals and directions without signals. If the angular distance between the channel paths is smaller than the beamwidth of the array, it will smear out the paths over many angles. The following example shows that Massive MIMO is not a guarantee for utilizing spatial sparsity.
The figure below considers a 64-antenna scenario where the received signal contains only three paths, having azimuth angles -20°, +30° and +40° and a common elevation angle of 0°. If the 64 antennas are vertically stacked (denoted 1 x 64), the signal gain seems to be the same from all azimuth directions, so the sparsity cannot be observed at all. If the 64 antennas are horizontally stacked (denoted 64 x 1), the signal gain has distinct peaks at the angles of the three paths, but there are also ripples that could have hidden other paths. A more common 64-antenna configuration is a 8 x 8 planar array, for which only two peaks are visible. The paths 30° and 40° are lumped together due to the limited resolution of the array.
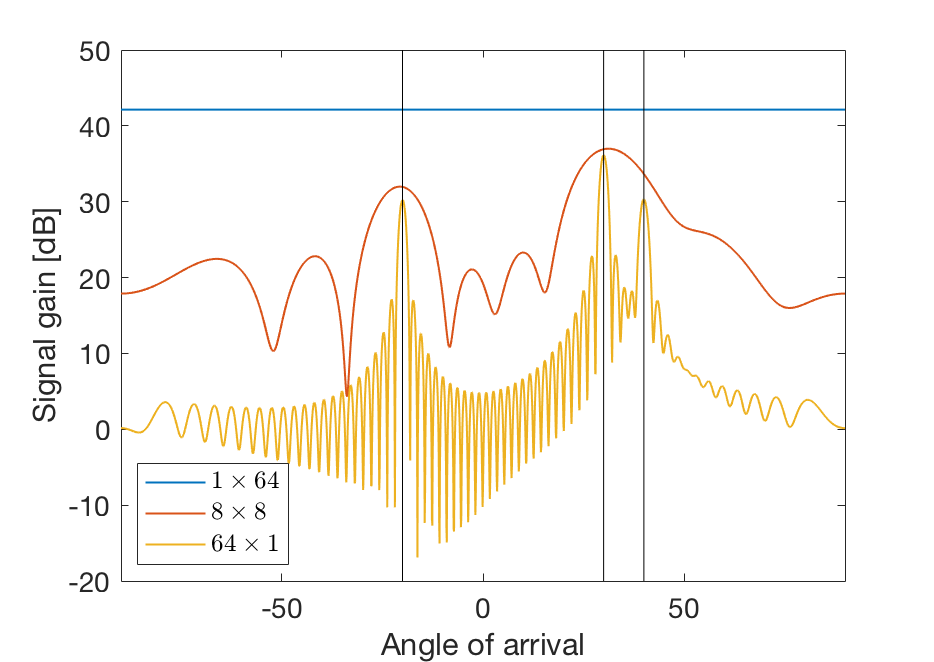
In addition to have a sufficiently high spatial resolution, a phase-calibrated array might be needed to make use of sparsity, since random phase differences between the antennas could destroy the structure.
Do we need sparsity?
There is no doubt that temporal and spatial sparsity exist, but not every channel will have it. Moreover, the transceiver hardware will destroy the sparsity unless a series of conditions are satisfied. That is why one should not build a wireless technology that requires channel sparsity because then it might not function properly for many of the users. Sparsity is rather something to utilize to improve the channel estimation in certain special cases.
TDD-reciprocity based Massive MIMO, as proposed by Marzetta and further considered in my book Massive MIMO networks, does not require channel sparsity. However, sparsity can be utilized as an add-on when available. In contrast, there are many FDD-based frameworks that require channel sparsity to function properly.
Reproduce the results: The code that was used to produce the plot can be downloaded from my GitHub.

The conclusion is that it is not always possible to utilise channel sparsity and one should not always depend on channel sparsity for channel estimation. Because 8×8 array and even 1×64 array are not able to utilise channel sparsity for channel estimation and only the 64×1 array can recognise channel sparsity.
There are other scenarios in which maybe 64×1 can not resolve the channel sparsity and then 1×64 or 8×8 array can resolve it better. So it can vary from case to case and there is not always different array geometries available for different cases. So if we can utilise channel sparsity with the available array geometry then it is better but it is not necessary and always possible to utilise channel sparsity for channel estimation.
My question is: How can channel sparsity be utilized in channel estimation? Without channel sparsity utilisation, will it be possible to do perfect channel estimation?
If you know the properties of the channel sparsity, you can use it as a prior in the channel estimation. For example, spatially sparse Rayleigh fading channels will have correlation matrices with many zero-valued eigenvalues. If you know the correlation matrix, you can improve the channel estimation by using an MMSE estimator. If you know that sparsity exists but not exactly where the zeros appear, there is a large theory on sparse estimation that can be utilized to find the zeros. There is plenty of work on both cases, particularly focused on FDD massive MIMO.
It is not possible to do perfect channel estimation in reality, but if sparsity exists and you utilize this information correctly, the estimation errors till reduce.
We have recently published a paper at SPAWC that proposes a channel estimation method that exploits sparsity only if it is present. The only required algorithm parameter is the thermal noise, which is known to the receiver. By using Stein’s unbiased risk estimate (SURE), we are able to denoise the channel optimally (in terms of the MSE), without any assumptions on the channel statistics (no assumption on channel gain, sparsity level, etc.). I feel that communication algorithms should always be implemented using such nonparametric methods to maximize robustness in practical scenarios.
A preprint that describes the algorithm we call BEACHES can be found here: https://arxiv.org/abs/1908.02884
The massive MIMO mmwave channel matrix can be assumed as low rank?
It depends on the number of antennas and propagation environment. It is common that people assume a spatially low-rank channel but (as discussed in this blog post) it does not always appear.
If I use sparse estimation (for estimating AoA) in your example that I will get better results, even though if I assume the local scattering channel model I would get some prior pieces of information that will be helpful for channel estimation and QoS for active UEs in the cell!
My question is: Is it practical that I use these prior pieces of information for random access protocols such as SUCR?
Sure, one should always make use of all the priors that are available. I’m quite sure that the vendors of Massive MIMO arrays are already trying to do this.
The practical problems are: 1) Which priors are general enough to cover all users in the cell? One can probably utilize the geometry of the array and some general aspects of the propagation environment, but we cannot expect all users to have the same sparsity pattern. Some users might be subject to rich scattering, while other might have very sparse LOS channels. 2) Algorithms that exploit sparsity are inherently unstable. The conditions for when the algorithms are guaranteed to converge to the right sparse solution are strict and likely not satisfied in practice. As a result, the algorithms will sometimes work very well and some time don’t work at all. This why it is hard to perform reliable interference mitigation with these techniques, if the algorithms should simultaneously exploit sparsity for 8 users.
Hi, professor Emil. Thank you for writing the book about massive MIMO Networks.
I have a doubt about the estimation of the channel correlation matrix R.
In your book (Massive MIMO Networks) the expression for MMSE is provided in equation (3.9), where the estimation of the channel h depends on the knowledge of the matrix R.
However, in order to obtain R, it is said in Section 3.3.3 that the equipment has to perform N observations of h. This, in my understanding, leads to a cyclic problem, i.e., in order to obtain R we need h, but to get h we need R.
My question is: How can the equipment observe h without knowing R in advance?
In our book, we assume that R is perfectly known since it is a statistical parameter, which means that it is fixed forever so one can easily learn it. This is the standard approach in communication theory; statistics are known, realizations of random variables are unknown.
However, in practice, it is more of a challenge to acquire R using limited resources. There are several different ways to do it. We provide an overview of such algorithms in this paper: https://arxiv.org/pdf/1904.03406
Hello Professor Emil – I cannot express enough how much I have gained technically reading through your blogs. At present, I am fundamentally struggling to understand why mmWave channels are sparse – is it because the transmitter’s AoD is narrow, and the lack of multi-path is due to the loss of signal when reflecting off objects? Also, how does channel sparsity impact SU-MIMO vs MU-MIMO from the transmitter’s point of view. Even if we have a sparse channel, co-polar elements should help us achieve SU-MIMO successfully. Would you say that is correct? And for MU-MIMO, I was trying to learn from above, it is difficult to conduct inter user interference cancellation between the targetted MU-MIMO users, as the pre-coder cannot be designed to overcome the challenge associated with ending up getting similar phase/amplitude at the users? My immense thanks in advance.