Beyond 5G, Commentary, Technical insights

Relative Value of Spectrum

22 Comments

What is more worth? 1 MHz bandwidth at 100 MHz carrier frequency, or 10 MHz bandwidth at 1 GHz carrier? Conventional wisdom has it that higher carrier frequencies are more valuable because “there is more bandwidth there”. In this post, I will explain why that is not entirely correct.

The basic presumption of TDD/reciprocity-based Massive MIMO is that all activity, comprising the transmission of uplink pilots, uplink data and downlink data, takes place inside of a coherence interval:

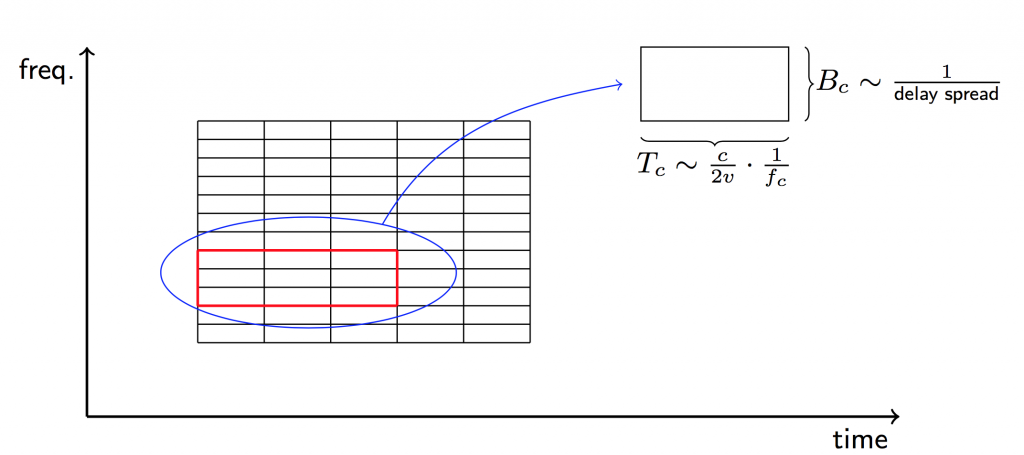
At fixed mobility, in meter/second, the dimensionality of the coherence interval is proportional to the wavelength, because the Doppler spread is proportional to the carrier frequency.

In a single cell, with max-min fairness power control (for uniform quality-of-service provision), the sum-throughput of Massive MIMO can be computed analytically and is given by the following formula:

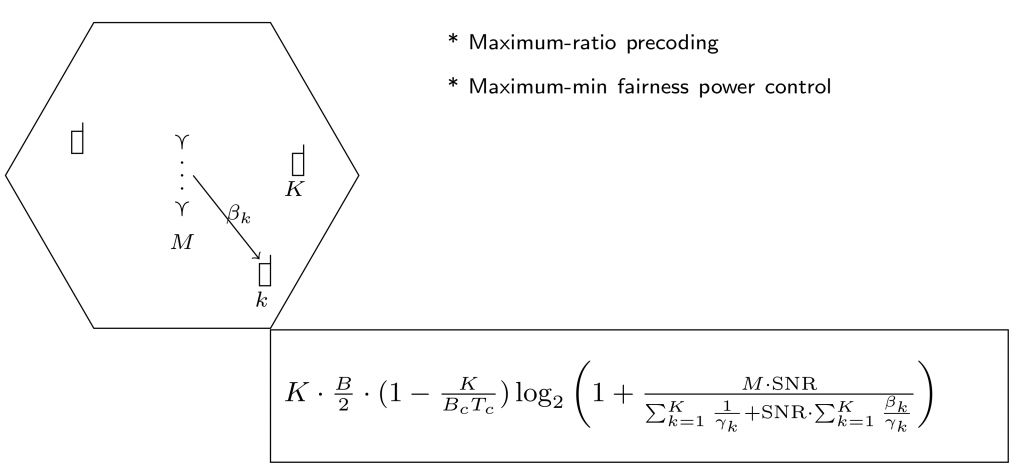
In this formula,

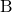  • $B$ = bandwidth in Hertz (split equally between uplink and downlink)
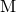  • $M$ = number of base station antennas
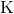  • $K$ = number of multiplexed terminals
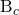  • $B_c$ = coherence bandwidth in Hertz (independent of carrier frequency)
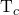  • $T_c$ = coherence time in seconds (inversely proportional to carrier frequency)
  • SNR = signal-to-noise ratio (“normalized transmit power”)
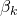  • $\beta_k$ = path loss for the k:th terminal
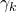  • $\gamma_k$ = constant, close to 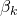$\beta_k$ with sufficient pilot power

This formula assumes independent Rayleigh fading, but the general conclusions remain under other models.

The factor that pre-multiplies the logarithm depends on $K$.
The pre-log factor is maximized when $K=B_c T_c/2$. The maximal value is $B B_c T_c/8$, which is proportional to $T_c$, and therefore proportional to the wavelength. Due to the multiplication $B T_c$, one can get same pre-log factor using a smaller bandwidth by instead increasing the wavelength, i.e., reducing the carrier frequency. At the same time, assuming appropriate scaling of the number of antennas, $M$, with the number of terminals, $K$, the quantity inside of the logarithm is a constant.

Concluding, the sum spectral efficiency (in b/s/Hz) easily can double for every doubling of the wavelength: a megahertz of bandwidth at 100 MHz carrier is ten times more worth than a megahertz of bandwidth at a 1 GHz carrier. So while there is more bandwidth available at higher carriers, the potential multiplexing gains are correspondingly smaller.

In this example,

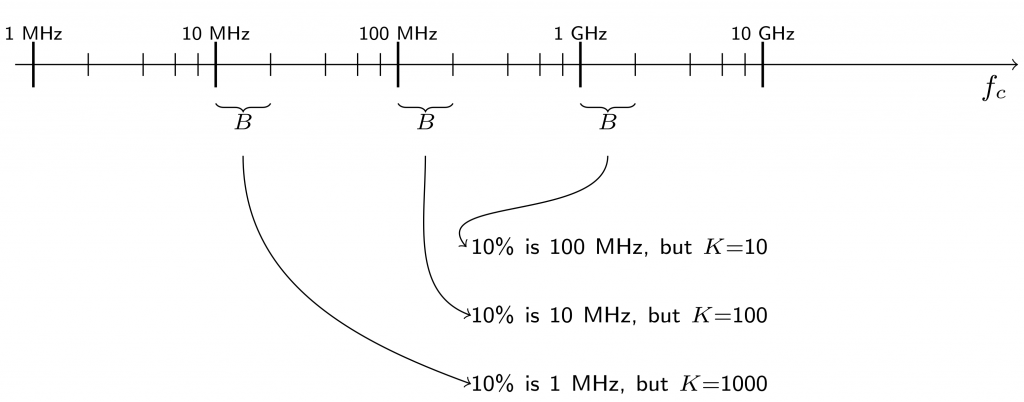
all three setups give the same sum-throughput, however, the throughput per terminal is vastly different.

22 thoughts on “Relative Value of Spectrum”

  1. This is a very interesting thinking, but the conclusion is based on the assumption of independent Rayleigh fading, when it comes to millimeter wave, LOS path will be the dominant , will the conclusion be a little different?

    Reply

    1. Yes, probably. At high enough frequencies, relying on reciprocity and “full measurements” of the channel may not be necessary.

      Reply

  2. Hi Erik, thanks, very interesting. So this suggests that the “sub 6 GHz” (In Europe e.g. the 2.6 GHz TDD and 3.4-3.8GHz TDD) bands could be the massive MIMO sweet spot for mobile operators. The wavelengths are short enough for practical macro base station antennas, and the massive MIMO spectral efficiency based on the above logic is much better than in the mmWave (26 GHz etc) bands. Right? Thanks

    Reply

    1. I tend to think that the sub-5 GHz bands would be the most valuable… Long coherence; good penetration of objects; mature hardware; arrays have attractive form factors; low phase noise… Not to diminish the value of mmWave access for certain applications however.

      Reply

      1. To what extent can the massive MIMO beam forming gain compensate for the relatively high indoor penetration loss of 3.5 GHz and above? 3.5 GHz mMIMO deployed on the 1800 MHz macro site grid: is it realistic to achieve similar indoor coverage in urban/dense urban environment as the 1800 MHz layers’ (without mMIMO)?

        Reply

        1. The beamforming can compensate for penetration losses, but one should not expect a full compensation. Say that the penetration loss can be 20 dB. You then need to go from 1 to 100 antennas to fully compensate by beamforming.

          Reply

          1. On data symbols that is. But to get the BF gain we need to have channel knowledge, and this will most likely be the limiting factor. The SNR per receiver will be 20dB lower.

          2. Correct: when “omnicasting” public channels to terminals for which no CSI is available, no beamforming gain is available. But this is not a fundamental problem, as the amounts of information that will be omnicasted are vastly smaller than the amounts of information that will be beamformed. May return to this matter in a future blog post.

          3. But to estimate the transmission weights based on UL reciprocity, the UL channel needs to be estimated before combining, hence the SNR per antenna will be at least 20dB below the combined signal.

          4. Sure. Reciprocity based beamforming works at low SNR, even though at *very* low SNR there is a squaring effect as the channel estimate mean-square value scales proportionally to received power. This is explained here, for example.

            In fact one of the paradoxes of reciprocity based Massive MIMO is that when adding more antennas, the number of unknown (channel coefficients) increases, yet performance monotonically increases.

  3. The discussions on the relative value of the spectrum are always interesting. Thank you. The message is clear but I was wondering if the results are completely “fair”. I mean, can we accept a throughput per terminal below a certain threshold? Is the assumption of scaling the number of antenna M with the number of users K realistic? At low frequencies large M could not be feasible….

    Reply

    1. We are far from the physical limits on the number of antennas that can be deployed in a cellular network. Instead of deploying all the antennas in a tower, one can spread the antennas over the facade of a building or some other large area. So I think the more important questions is how large K will be in a practical scenario.

      Reply

      1. Sure, but I was also considering the perspective of an operator that operates in a context where there can be a lot of constraint or limitations (EMF regulation, visual impact, site accessibility for maintenance, costs and many others..), so what you would like to do sometime does not match with what you can in practice do. Anyway you’re right, distributed antenna could be the way.

        Reply

  4. Erik, I am not comfortable enough with the assumption that the coherence bandwidth B_c is independent of the carrier bandwidth. At mm-waves, you’ve got only a few dominant paths which render the rms delay spread rather small, therefore boosting B_c.

    Reply

    1. You’re raising a good question. Clearly, if it is known a priori where to point the beam, the coherence bandwidth is much larger. But if it isn’t known a priori where to point the beam, then the coherence bandwidth might not be different at higher bands. (Recall the two-path model, Chapter 2 – only the difference in path lengths matters.) Authoritative papers, e.g., this one, claim that “Since (outdoor) coherence bandwidths of mm-Wave channels are similar to those of microwave channels [4], [33], the overall challenges of CSI feedback overhead are then comparable to those of higher-mobility (vehicular) microwave massive-MIMO systems.”

      It should however be stressed that the specific formula (and its implications) given are valid for independent Rayleigh fading. At higher bands, the channel is increasingly line-of-sight-like, or more easily parameterized/sparse, so estimation of the complete response becomes unnecessary, and – importantly – that may affect the required pilot overhead.

      Reply

  5. Systems that operate at high frequencies (e.g., mmwave) will likely be at short range, in small cells with lower mobility. Roughly speaking, an order of magnitude increase in frequency likely will be accompanied by an order of magnitude decrease in mobility. An order of magnitude increase in bandwidth likely will be accompanied by an order of magnitude decrease in delay spread, so maybe in the end it’s a wash?

    In any case, I think we’ll continue to see large-scale coverage with sub-5GHz frequencies, with underlay coverage in small cells at higher and higher frequencies depending on size and user mobility.

    Reply

    1. Yes, there are exact throughput expressions for maximum ratio processing and approximate expressions for zero-forcing processing. The former can be found in https://arxiv.org/abs/1805.07972 and the latter is found in the reference list of that paper.

      Reply

  7. Hello
    According to the definition of massive MIMIO in the massive MIMO network book, massive MIMO uses SDMA to serve all user in the same time-frequency resources to achieve a multiplexing gain.
    Can we say that this definition is limited to the users in only a coherence block and we use FDMA to serve more users?
    Thank you.

    Reply

    1. No, FDMA and TDMA corresponds to serving one user per coherence block (but a different one in different coherence block).

      In Massive MIMO (and SDMA), we serve all the users in all coherence blocks.

      Reply

      1. Thank you for your answer.
        What we can say about using the subcarriers? Do all users, in a massive MIMO system utilize all subcarriers?

        Reply

        1. Yes, each coherence block contains several subcarriers, as explained Chapter 2 of Fundamentals of Massive MIMO.

          Reply

Leave a Reply

Your email address will not be published. Required fields are marked *