Last year, I wrote a post about channel hardening. To recap, the achievable data rate of a conventional single-antenna channel varies rapidly over time due to the random small-scale fading realizations, and also over frequency due to frequency-selective fading. However, when you have many antennas at the base station and use them for coherent precoding/combining, the fluctuations in data rate average out; we then say that the channel hardens. One follow-up question that I’ve got several times is:
Can we utilize the channel hardening to estimate the channels less frequently?
Unfortunately, the answer is no. Whenever you move approximately half a wavelength, the multi-path propagation will change each element of the channel vector. The time it takes to move such a distance is called a coherence time. This time is the same irrespectively of how many antennas the base station has and, therefore, you still need to estimate the channel once per coherence time. The same applies to the frequency domain, where the coherence bandwidth is determined by the propagation environment and not the number of antennas.
The following flow-chart shows what need to happen in every channel coherence time:
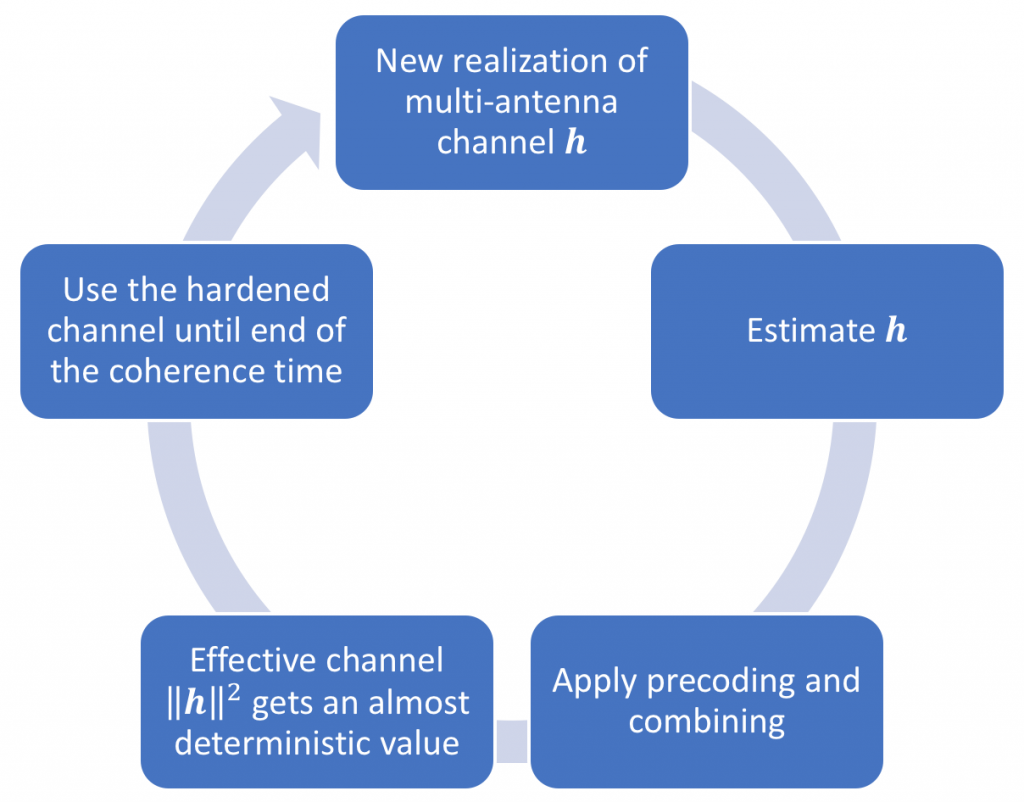
When you get a new realization (at the top of the flow-chart), you compute an estimate (e.g., based on uplink pilots), then you use the estimate to compute a new receive combining vector and transmit precoding vector. It is when you have applied these vectors to the channel that the hardening phenomena appears; that is, the randomness averages out. If you use maximum ratio (MR) processing, then the random realization h1 of the channel vector turns into an almost deterministic scalar channel ||h1||2. You can communicate over the hardened channel with gain ||h1||2 until the end of the coherence time. You then start over again by estimating the new channel realization h2, applying MR precoding/combining again, and then you get ||h2||2 ≈ ||h1||2.
In conclusion, channel hardening appears after coherent combining/precoding has been applied. To maintain a hardened channel over time (and frequency), you need to estimate and update the combining/precoding as often as you would do for a single-antenna channel. If you don’t do that, you will gradually lose the array gain until the point where the channel and the combining/precoding are practically uncorrelated, so there is no array gain left. Hence, there is more to lose from estimating channels too infrequently in Massive MIMO systems than in conventional systems. This is shown in Fig. 10 in a recent measurement paper from Lund University, where you see how the array gain vanishes with time. However, the Massive MIMO system will never be worse than the corresponding single-antenna system.

Fully agree on all points. But it might be worth pointing out that hardening isn’t necessary for massive MIMO to work. Granted, hardening is useful: 1) it makes the simple (use-and-forget) capacity bounds rather tight, 2) it eliminates the need for downlink pilots in a simple way, 3) it simplifies resource allocation, and 4) it improves reliability (in absence of time/frequency diversity, the effective diversity order will be the rank of the channel covariance matrix). However, reciprocity-based beamforming, the core principle of massive MIMO, works also in environments without any hardening at all.
Maybe I’m missing some points here.
As UEs could not practically perform beamforming in uplink direction their ability to communicate in common freq-time resources in uplink direction relies on optimal performance of MRC in BS due to channel hardening, without channel hardening MRC fails separating their data symbols, hence I guess hardening might be necessary at least for uplink communication if UEs are supposed to be communicating simultaneously in common frequency bands.
Thank you.
Channel hardening is a desirable property since the performance becomes predictable, but it is not a necessity in Massive MIMO and it doesn’t help the BS to separate users.
If you replace “channel hardening” with “favorable propagation” (i.e., the users’ channel vectors are nearly orthogonal) in your post, your conclusions will basically be true. You can read more about these properties in Section 2.5 of my book Massive MIMO Networks.
Thanks a lot.
As you mentioned I had confused the favorable propagation condition with channel hardening phenomenon.