We have now released the 39th episode of the podcast Wireless Future. It has the following abstract:
Massive bandwidths are available in the sub-terahertz bands, but the coverage of a cellular network exploiting those frequencies will be spotty. The 6GTandem project tries to circumvent this issue by developing a dual-frequency system architecture that jointly uses the sub-6 GHz and sub-THz bands. In this episode, Erik G. Larsson and Emil Björnson are visited by Dr. Parisa Aghdam, Technical Lead of 6GTandem and Research Manager at Ericsson. The discussion starts with potential use cases, such as extended reality services in stadiums and connected factories. The conversation then focuses on hardware aspects, such as how to build a distributed antenna system using plastic microwave fibers and amplifiers so that sub-THz signals can be transmitted from many different locations. You can read more about the EU-funded project and its partners at https://horizon-6gtandem.eu/
You can watch the video podcast on YouTube:
You can listen to the audio-only podcast at the following places:
The research community often praises reconfigurable intelligent surfaces (RISs) as a transformative technology. By controlling parts of wireless propagation channels, we can improve the bit rates by increasing the received signal strength, mitigating interference, enhancing channel ranks, etc. The potential benefits RISs can bring to wireless networks are now well documented, and several of them have also been demonstrated experimentally. However, the RIS technology also introduces several practical complications that one must be mindful of. In this blog post, I will give two examples of the dark side of the RIS technology.
Pilot contamination between operators
Suppose a telecom operator deploys an RIS to enhance the performance experienced by its customers. The academic literature is full of algorithms that can be used to that end. Each time the operator changes the RIS configuration, it will affect not only the wireless channels within its licensed frequency band but also the channels in many neighboring bands. The phase-shifting in each RIS element acts as an approximately linear-phase filtering operation, which shifts the phases of reflected signals (proportionally to their carrier frequencies) both in the intended and adjacent bands. Since there is no non-linear distortion, the operator’s wireless signals are maintained in their designated band. Nevertheless, the operator messes with the channel characteristics in neighboring bands every time it reconfigures its RIS. In the best-case scenario, the systems operating in neighboring bands only experience additional fading variations. In the worst-case scenario, they will suffer from substantial performance degradation.
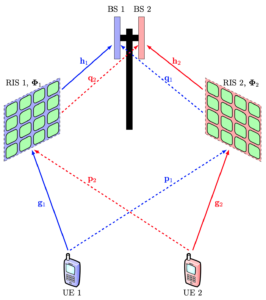
An instance of the latter scenario appears when two telecom operators deploy RISs in the same coverage area. We studied this scenario in a recent paper. 5G networks typically use time-division duplex (TDD) bands, and the operators are time-synchronized, so they switch between uplink and downlink simultaneously. This implies that the considered operators will send pilot sequences in parallel, which is usually fine because they are transmitted in different bands. However, if each operator uses its pilot sequences for RIS reconfiguration that helps its own users, it will also modify the other operator’s channels in undesired ways after the estimation has occurred. This leads to a new kind of pilot contamination effect, which differs from that in Massive MIMO but leads to the same bottlenecks: reduced estimation quality and a performance limit at high signal-to-noise ratios (SNRs). Consequently, if a large-scale deployment of RIS occurs in cellular networks, we will see not only the intended performance improvements but also occasional unexpected degradations. More research is needed to quantify this effect and what can be done to mitigate it.
Malicious RIS
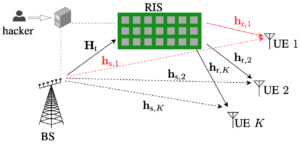
While the pilot contamination caused between telecom operators is an unintentional disturbance, RIS could also be used for intentional “silent” jamming. In a recent paper, we analyze the situation where a hacker takes control of an operator’s RIS and turns it into a malicious RIS. Instead of maximizing the received signal strength at a specific user device, the RIS can be configured to minimize the signal strength. Since this is achieved by causing destructive interference over the air, the user device will perceive this as having poor coverage. Conventional jamming builds on sending a strongly interfering signal to prevent data decoding, and this can be easily detected. By contrast, the silent jamming caused by a malicious RIS is hard to detect since it destroys the channel without introducing new signals. In our paper, we demonstrate how a malicious RIS can avoid detection by only destroying the channel for one user device while other devices are unaffected. We also show that malicious reflection is possible even if the RIS has imperfect channel knowledge.
In summary, there is a dark side to the RIS technology. It can both manifest itself through unintentional tampering with the channels in neighboring frequency bands and through the risk that an RIS is hacked and turned into a malicious RIS that degrades rather than improves communication performance. Careful regulation, standardization, hardware design, and security will be required to overcome these challenges.
I receive many questions from students and researchers on social media, including this blog, YouTube, and ResearchGate. I do my best to answer such questions while commuting to work or having few minutes between meetings. I receive some questions quite frequently, making it worth creating videos where I try to answer them once and for all.
Below, you can find the first video in that series, and it answers the question: How many beams can you send from a MIMO array? As you will notice when watching the video, we obtain a more appropriate question if “can you send” is replaced by “do you want to send”.
If you have remaining doubts or comments after watching it, please feel free to post a comment on YouTube.
Several 6G-related edited books have recently been published, which highlights the fact that the 6G-related research has now progressed for at least five years. Although the standardization is yet to begin, we know quite well which new technology components will be on the agenda. This does not mean that everything that is being researched will eventually be used—far from it—but we can be quite sure that 6G will build on a subset of them.
I have co-authored a chapter in the new book Fundamentals of 6G Communications and Networking, published by Springer and edited by Xingqin Lin, Jun Zhang, Yuanwei Liu, and Joongheon Kim. The book contains chapters about 6G visions and tutorials on new waveforms, coding and access schemes, integrated communication and sensing, reconfigurable intelligent surfaces, cell-free networks, non-terrestrial networks, semantic communication, and different aspects of AI.
My contribution was a chapter on Near-Field Beamforming and Multiplexing, written with Parisa Ramezani. We describe how previously negligible physical phenomena become essential when making the antenna arrays larger in future networks. These radiative near-field effects impact everything from pathloss modeling to the physical shapes of transmitted signals and the ability to spatially multiplex many user devices. If you are unfamiliar with these effects, I recommend reading our chapter. We summarize the technical insights and fundamentals from a few recent papers and tell the complete story around it. In a way, it is the detailed version of the following video tutorial:
What is the reason to write a book chapter?
The good thing about writing a book chapter, compared to a tutorial article for a scientific journal, is that you get much freedom to organize it in the way you find most pedagogical. You are typically invited to write a chapter based on your expertise and trusted in your ability to do so; thus, the review process is friendly and constructive.
The fact that your chapter is grouped together with those written by other experts could be a good way of attracting readers. However, one must be cautious because some publishers are particularly greedy when it comes to copyright: they might ban you from ever uploading a preprint to your homepage or arXiv. This happened to me with a chapter about energy-efficient communications in a book published by IET, with the result that it has probably only been read by a handful of people and has no citations. This is because few researchers and universities pay for access to the IET database, and even fewer buy printed books these days. In retrospect, it was clearly not worth the effort put into the writing process—we don’t even get money from book sales. This happened in 2019, but despite the push toward Open Science, there are other publishers that behave badly. Two years ago, I was asked to write a chapter for a book on reconfigurable intelligent surfaces under the same bad conditions, but this time, I was aware of the issue and declined.
Springer is one of the more reasonable open publishers, which allows you to share the preprint immediately and then share the final author version one year after publication. This is at least a step in the right direction.
The way that mobile communication networks are designed changed dramatically with the advent of 5G. In the past, it was all about utilizing large bandwidths and deploying many base stations. Nowadays, we are instead equipping each base station and smartphone with multiple antennas, which enables us to use signal processing algorithms to improve signal strength, enhance reliability, and send more data of the same spectrum by controlling the spatial direction of each signal layer. In essence, we refine the hardware and algorithms instead of deploying more infrastructure and requiring more signal resources.
Further dramatic changes are envisioned in the 6G era, where the use of even larger antenna arrays uncovers near-field effects, conventional frequency bands will be complemented with millimeter and sub-terahertz spectrum, optimized reflections from reconfigurable surfaces might improve propagation conditions, and communication networks can provide new localization and sensing services.
These extraordinary changes will affect not only the wireless technology but also the required knowledge and skills among the engineers and researchers who will implement it. Hence, it is essential to revise the curriculum in basic wireless communication courses to shift focus onto these new aspects of the physical layer.
When I realized the need for a new basic textbook, I joined forces with Özlem Tuğfe Demir to write “Introduction to Multiple Antenna Communications and Reconfigurable Surfaces”, NowOpen (2024). The book provides a gentle introduction to multiple antenna communications with a focus on system modeling, channel capacity theory, algorithms, and practical implications. The reader is expected to be familiar with basic signals and systems, linear algebra, probability theory, and digital communications, but a comprehensive recap is provided in the book. Once the fundamental point-to-point and multi-user MIMO theory and its practical implications have been covered, we also demonstrate how similar methodologies are used for wireless localization, radar sensing, and optimization of reconfigurable intelligent surfaces.
The first draft of the book was written for the first-year Master course TSKS14 Multiple Antenna Communications at Linköping University. You might have seen the YouTube video series that I produced while teaching that course during the pandemic. The book covers the same things and much more, and it contains numerous new examples and exercises.
The writing process focused on pinpointing all the technical and practical know-how that we believe the next-generation wireless engineers must have within this topic. We then wrote the text as a story that leads to these points. The writing has taken a long time: four years of progressive course material development followed by two years of intense writing with the goal of completing a book.
The book is published with open access and accompanying MATLAB code that reproduces all the simulation results. You can access the PDF from the publisher’s website, where you can also buy printed copies. We are extremely proud of the book and hope you will like it too!
We have now released the 38th episode of the podcast Wireless Future. It has the following abstract:
Many topics are studied within the 6G research community, from hardware design to algorithms, protocols, and services. Erik G. Larsson and Emil Björnson recently attended the ELLIIT 6G Symposium in Lund, Sweden. In this episode, they discuss ten things that they learned from listening to the keynote speeches. The topics span from integrated sensing, positioning, and localization via machine-learning applications in communications to fundamental communication theory, such as circuits for universal channel decoding and jamming protection. The expected 6G spectrum ranges, energy efficiency in base stations, and new use cases for electromagnetic materials are also covered.You can find slides from the symposium here.
Ten things we learned
3:22 Integrated sensing and communication 12:45 Positioning using phase-coherent access points 20:42 Experimental work on positioning from ELLIIT Focus period 24:02 Trained activation functions in machine learning 30:25 Learning to operate a reconfigurable intelligent surface 37:15 Guessing Random Additive Noise Decoding (GRAND) 44:30 Protecting digital beamforming against jamming 53:02 6G frequency spectrum 1:01:50 Energy efficiency in base stations 1:08:47 New use cases for electromagnetic materials
You can watch the video podcast on YouTube:
You can listen to the audio-only podcast at the following places:
The golden frequencies for wireless access are in the band below 6 GHz. Why are these frequencies so valuable? The reasons, of course, are rooted in the physics. First, the wavelength is short enough that a (numerically) large array has an attractive form factor, enabling spatial multiplexing even from a single antenna panel. At the same time, the wavelength is large enough that a sufficiently large aperture can be obtained with a reasonable number of antennas – which, in turn, directly translates into a favorable link budget and high coverage. Second, below 6 GHz, Doppler is low enough, even at high mobility, that reciprocity-based beamforming based on uplink pilots for channel estimation works without relying on prior assumptions on the propagation environment, let alone on the fading statistics. This directly translates into robustness, simplicity of implementation, and scalability with respect to the number of service antennas. Third, these frequencies are not hindered so much by blockage, and strong multipath components can guarantee connectivity even when there is no line-of-sight, while in contrast, for mmWave a human blocking the line-of-sight path can suffice to break the link. Finally, analog microelectronics for the golden bands is mature, and very energy-efficient.
Distributed MIMO (D-MIMO) with reciprocity-based beamforming is the natural way of best exploiting the golden frequencies. This technology naturally operates in the [geometric] near-field of the “super-array” collectively constituted by all antenna panels together. In fact, the actual antenna deployment hardly matters at all! With reciprocity-based beamforming, the physical shape of the actual beams, and grating lobe phenomena in particular, become irrelevant. If anything, given a set of antennas, it is advantageous to spread them out over as large aperture as possible. The only definite no-no is to place antennas closer than half a wavelength together: such dense packing of antennas is almost never meaningful, as sampling points lambda/2-spaced apart captures essentially all the degrees of freedom of the field; putting the antennas closer results in coupling effects that are usually of more harm than benefit.
REINDEER is the European project that develops and demonstrates D-MIMO for the golden frequencies. What are the most important technical challenges? One is, down-to-earth, to handle the vast amounts of baseband data, and process them in real time. Another is time and phase synchronization of distributed MIMO arrays: antenna panels driven by independent local oscillators must be re-calibrated for joint reciprocity every time the oscillators have drifted apart. Locking the clocks using cabling is possible in principle, but considered very expensive to deploy. A third is initial access, covering space uniformly with system information signals, and waking up sleeping devices. A fourth is energy-efficiency, at all levels in the network. A fifth is the integration of service of energy-neutral devices that communicate via backscattering. D-MIMO naturally offers the infrastructure for that, permitting simultaneous transmission and reception from different panels in a bistatic setup; however, these activities break the TDD flow and must be carefully integrated into the workings of the system.
If sub-6 GHz are gold, then what is silver? Perhaps right above: the 7-15 GHz band, that is intended in 6G to extend the “main capacity” layer. It appears that these bands can still be suitable mobile applications, and that higher carriers (28 GHz, 38 GHz) are appropriate for fixed wireless access mostly. But the sub-6 GHz bands will remain golden and the first choice for the most challenging situations: high mobility, area coverage, and outdoor-to-indoor.
