One word that is tightly connected with Massive MIMO is pilot contamination. This is a phenomenon that can appear in any communication system that operates under interference, but in this post, I will describe its basic properties in Massive MIMO.
The base station wants to know the channel responses of its user terminals and these are estimated in the uplink by sending pilot signals. Each pilot signal is corrupted by inter-cell interference and noise when received at the base station. For example, consider the scenario illustrated below where two terminals are transmitting simultaneously, so that the base station receives a superposition of their signals—that is, the desired pilot signal is contaminated.
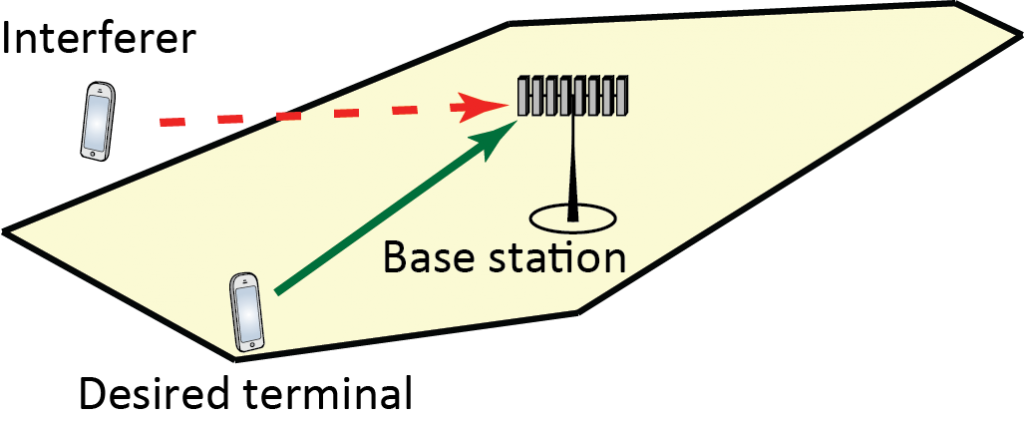
When estimating the channel from the desired terminal, the base station cannot easily separate the signals from the two terminals. This has two key implications:
First, the interfering signal acts as colored noise that reduces the channel estimation accuracy.
Second, the base station unintentionally estimates a superposition of the channel from the desired terminal and from the interferer. Later, the desired terminal sends payload data and the base station wishes to coherently combine the received signal, using the channel estimate. It will then unintentionally and coherently combine part of the interfering signal as well. This is particularly poisonous when the base station has M antennas, since the array gain from the receive combining increases both the signal power and the interference power proportionally to M. Similarly, when the base station transmits a beamformed downlink signal towards its terminal, it will unintentionally direct some of the signal towards to interferer. This is illustrated below.
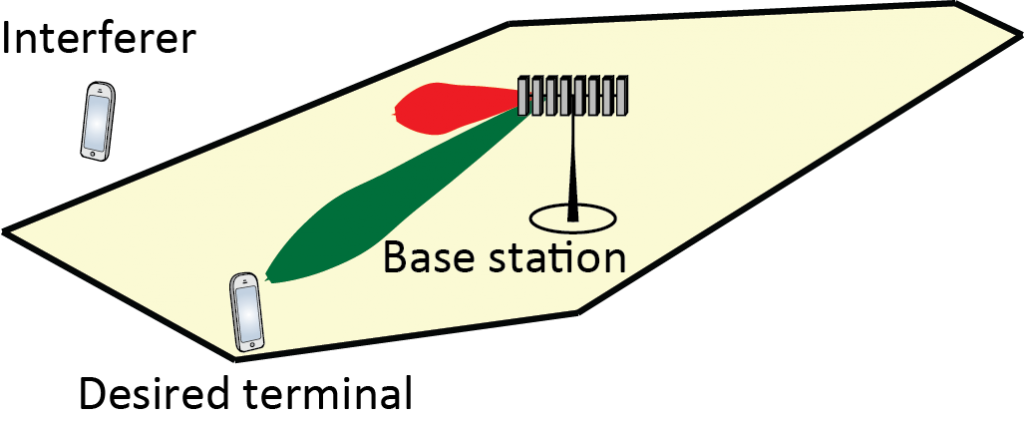
In the academic literature, pilot contamination is often studied under the assumption that the interfering terminal sends the same pilot signal as the desired terminal, but in practice any non-orthogonal interfering signal will cause the two effects described above.

If non-orthogonal pilot sequences also cause pilot contamination, how about using random pilots ? What is overall impact ?
Random pilots lead to pilot contamination as well. For each realization of the random pilots, you will get a set of pilot sequences that is either orthogonal or non-orthogonal. Then the pilot contamination effect follows in the same way as for deterministic pilots.
The potential benefit of having random pilots is that you can “share” the pilot contamination between the users, so that everyone get an equal share on average. However, since cell-edge users are more sensitive to pilot contamination than cell-center users, you might want to coordinate the pilot allocation across cells instead of randomize it. In that sense, random pilots is the baseline scheme that any “smart” scheme should be able to beat.
Thank you for the this interesting topic.
I would only like to inquire what is specific for Massive MIMO systems? Pilot contamination can occur in any cellular system. So, is the only difference the limited number of orthogonal pilot signal due to the massive antenna array?
Thank you
Massive MIMO is supposed to serve tens of users simultaneously, instead of one or a few as in conventional cellular networks. Hence, for a given number of orthogonal pilots, each pilot needs to be reused more frequently in space. That is why the pilot contamination interference caused by pilot reuse might have a greater impact in Massive MIMO.
The number of antennas does not affect the required number of pilots, if we use TDD and channel reciprocity.
I need some explanation on coherence interval and how to calculate it? I also wonder what is the covariance matrix?
The coherence interval is explained in many books and papers. One freely available source is the following book chapter:
http://www.diva-portal.org/smash/get/diva2:1049059/FULLTEXT02.pdf
Its dimensionality is the product of the coherence time and the coherence bandwidth. You can check out Chapter 2 in “Fundamentals “Fundamentals of Massive MIMO” or “Massive MIMO Networks” for details on how to compute these parameters in different scenarios. I think Fundamentals of Wireless Communications also contain discussions about this.
The covariance matrix of a random channel h is E{(h-E{h})(h-E{h})^H}, where E{} stands for expectation.
Thank you sir, really appreciate it.
What is the relationship between the length of a coherent interval and speed of a user equipment in massive MIMO? To be specific in Zhu et., al (2016) SPR and MBD technique! I want to validate my result with their work using the same base parameters but with my own developed model. Thank you.
The length of the coherence interval is the product of the coherence bandwidth and the coherence time. These parameters depend on the carrier frequency, user speed, and propagation environment, and is the same irrespective of single-antenna or massive MIMO communication.
You can find examples of how to compute the coherence time and coherence bandwidth in Fundamentals of Wireless Communications, which is freely available here: https://web.stanford.edu/~dntse/wireless_book.html
You can also find a detailed explanation in the book “Fundamentals of Massive MIMO” and a short description in the book “Massive MIMO Networks”.
“When estimating the channel from the desired terminal, the base station cannot easily separate the signals from the two terminals…”
Is it possible for each pilot signal to have a unique signature…..
Yes! This is called orthogonal pilot sequences and is normally assumed to be used within each cell in Massive MIMO.
Hi!
So if we use orthogonal pilot sequences, what methods would we use to remove these pilots? This is what I mean:
We have four users, each having orthogonal pilot sequences, who transmit at the same time to the BS. Now the BS receives a superposition of the four (faded) pilots, plus some amount of noise. What would be the usual process to estimate the four users’s channels? If we attempt to estimate each channel individually, I think we will still have to deal with all the “interference” from the pilots in spite of orthogonality. Do we use some kind of joint estimation technique? Any sources you could point me to would be great!
Thank you for the informative article!
If the pilot sequences are orthogonal, you can correlate the received signal with the pilot sequence of one of the users. The interfering pilots disappear in that process. You will then have a received signal that only contains that desired user’s channel plus noise.
See Section 3 in Massive MIMO Networks for details: https://massivemimobook.com
Hi! Thank you for the clarification. The book is a great read! However, I am having some trouble understanding the model (3.1) in the linked book. I went through the previous chapters as well, but since we use some different conventions I am having trouble with this.
As per my understanding, Y_ j^p (which I will call Y for convenience) is an M_ j by tau_p received matrix. From what I could understand, the rows of this matrix correspond to different antennae in the base station, while the columns correspond to different instants in time. We have tau_p different instances, corresponding to tau_p different pilot symbols. Now, are we assuming here that all multipath components arrive at the same time in the base station? This is what I am lead to believe according to eq. 2.21.
From what I could understand, all UEs are synchronized. Now, they will be spread out in the cell, with different UEs being in different positions in the cell. If they begin transmission at the same time, their signals will be received at different times at the BS. So, the tau_p samples of UE1 will be arriving at a different time as compared to the tau_p samples of UE2 and so on. So even if we assume we have no multipath, I don’t understand how we only have tau_p columns for Y. Wouldn’t the ‘spread’ caused due to different UE positions (relative to the Base station) cause signals to arrive at different times?
Are we assuming that the UE signals arrive at the same time at the Base Station in addition to there being a single path? I am a bit confused as to how the UEs could be synchronized to make their signals arrive at the same time at the base station.
Sorry for the long post. Hope you can clarify! Thank you once again for the informative blog and the book!
So from your explanation pilot signals are affected by two factors:
1. Inter-cell interference
2. Noise in the channel
Does it also mean there is no way to know which pilot signal arrives first at the BS?
Just thinking about it.
The users are typically time synchronized with the base station in such a way that the signals are received at approximately the same time. There are still some small time differences, but you cannot exploit these to do something smart unless you know them, and you cannot know them without estimating them. It is a chicken-and-egg problem…
In a limited setting of a single cell:
Can pilot contamination be neglected, with orthogonal sequences allocated (feasible since there are only tens of active users)?
Or does it still need to be considered as an inter-user interference?
Yes! Most papers on single-cell Massive MIMO are considering a setup without pilot contamination, motivated in the way that you suggested.
Is there any need to do comparative analysis of fading models in massive MIMO before choosing a particular model? Or is the Rayleigh fading model generally adopted?
Many academic papers consider i.i.d. Rayleigh fading, since it leads to tractable and intuitive expressions. But practical channels will not be i.i.d. Rayleigh fading, so there is a need to evaluate other more realistic models to figure out if there are any substantial differences. In my recent book “Massive MIMO Networks”, we show how to analyze correlated Rayleigh fading. We also use 3GPP channel models to carry out realistic simulations.
Why do you assume that you have only one channel gain between the user and the antenna (flat-fading channel), but in the frequency selective case, there is an attenuation for each frequency, and we will have multiple channel gains for each frequency. Does this change the result of spectral efficiency for example in the presence of pilot contamination?
Most communication systems are indeed designed for frequency-selective channels, but the common approach is to use multi-carrier modulation to split the frequency-selective channel into many frequency-flat subchannels/subcarriers. Chapter 2 in Fundamentals of Massive MIMO provides a good explanation of that.
Thanks!
Thank you for the last suggestion. I read Chapter 2 in Fundamentals of Massive MIMO. Always concerning the OFDM associated to Massive MIMO and the fact that one complex gain is used between any pair of antennas. If I understood it correctly, the condition is that the slot duration is equal to the channel coherence time, then each coherence interval spans Nsmooth subcarriers and Nslot consecutive OFDM symbols. So the bandwidth are splitted into N subcarriers but only Nsmooth subcarriers are used. Is it true?
Concerning the question on Chapter 2: “So the bandwidth are splitted into N subcarriers but only Nsmooth subcarriers are used. Is it true?”
No. The entire system bandwidth, B0, is used. Effectively multiple consecutive coherence intervals are used simultaneously. But each coherence interval can be treated independently in the analysis. See figures 2.4 and 2.6.
Good day prof. Please I need a suggestion on what other matrices can be use to separate users sharing the same pilot sequence apart from Hadamard matrix.
Any unitary matrix will be equally good from a theoretical perspective, but there might be implementation aspects that may some more useful than others. An alternative to a Hadamard matrix is a DFT matrix or Zadoff-Chu sequences. This is briefly discussed in Section 3.1.1 of the book Massive MIMO Networks.
thank prof
Hello sir, I read in one of the journals on acquiring channel state information in massive MIMO that someone can reduce the computational complexity by whitening (projecting into signal subspace) the received signal vector. My question here is: how do you whiten such a signal? and is there any method someone can use to reduce the computational part from the stated above. I anticipate your kind response. thank you.
I don’t know which journal paper you are referring to. Whitening and projecting onto the signal space are actually two different things. I don’t think whitening by itself will reduce complexity – it is just an implementation detail. Projecting onto the signal space could potentially reduce the complexity of the remaining tasks, but you need to know the signal space for it to work.
I don’t think we need to worry much about the computational complexity, but first find the type of processing that performs the best and then find an efficient implementation of it.
Thank you prof. I really appreciate.
Does massive MIMO depend on spatial multiplexing or spatial diversity? If both, I need an explanation!
Strictly speaking, it doesn’t require any of these things, but:
a) The largest throughput gains from Massive MIMO comes from using it for spatial multiplexing. (http://ma-mimo.ellintech.se/2018/03/23/a-basic-way-to-quantify-the-massive-mimo-gain/)
b) The channel hardening property is a consequence of spatial diversity. (http://ma-mimo.ellintech.se/2017/01/25/channel-hardening-makes-fading-channels-behave-as-deterministic/)
Sir, what particular property of a unitary matrix makes it a better candidate for implementation purpose than another one?
That depends on what the unitary matrix is going to be used for. For example, when using a unitary matrix as pilot matrix, it is good if all the elements in the matrix have the same magnitude. You can read more about that in Section 3.1.1 of my book Massive MIMO Networks.
In multi-cell systems, we cannot assign orthogonal pilot
sequences for all users in all cells, Due to the limitation of
the channel coherence interval.
Could you explain why coherence interval has a limitation?
What are the present open research problems in pilot contamination in MIMO system?
Most things have already been solved since many people have considered this problem the last 5-10 years. See this blog post for an outline of different approaches: http://ma-mimo.ellintech.se/2017/06/25/approaches-to-mitigate-pilot-contamination/
In particular, the paper “Massive MIMO has unlimited capacity” shows that utilization of spatial correlation information is key to solving the pilot contamination problem. This raises the question: How can we acquire such spatial correlation information in real systems with many antennas? Some first attempts to do that have been outline in the recent overview paper “Towards Massive MIMO 2.0: Understanding spatial correlation, interference suppression, and pilot contamination” (https://arxiv.org/abs/1904.03406)
Does SUCR protocol performs well for the other fading channels like rician, eta-mu, etc channels? If we combine SUCR-TA-IPA, is there any significant improvement in the collision resolution probability than the basic SUCR scheme?
I believe that the SUCRe protocol will work well along with most fading channel models, but it works better the more channel hardening and favorable propagation that channel provide.
I’m not familiar with SUCR-TA-IPA.
Good day Prof. Emil, I need some clarification and suggestions on the following issues. For mMIMO based systems under pilot attack:
1) What is the basic limit of secure communication?
2) Are there any unified transmission schemes which are effective for general MIMO channels and how can transmission schemes be integrated for general real mMIMO channels?
3) How can one design a secure transmission schemes in practical communication systems.
4) How can one achieve the design of a physical layer security in mMIMO systems, for the implementation of combined mMIMO secure transmission scheme with other vital 5G technologies such as secure mm-wave mMIMO communications and massive communication in heterogeneous networks.
1) The overview paper “Massive MIMO for next generation wireless systems” contains a guess that Massive MIMO systems are more secure than conventional systems, but that seems not to be the case under jamming attacks. This is explained by Erik G. Larsson in this blog post: http://ma-mimo.ellintech.se/2018/05/07/i-was-wrong-two-incorrect-speculations/
2) You can find a summary of all the main transmission schemes in Chapter 4 of my book “Massive MIMO networks” (https://massivemimobook.com).
3) There are no perfectly secure transmission schemes, but in Massive MIMO one can potentially use the spatial domain to make the system more secure. I recommend you to read these papers: https://arxiv.org/pdf/1504.07154 and https://arxiv.org/pdf/1702.08800.pdf
4) I don’t think there is a known answer to that, but it is a good research direction.
Good day sir, I need some explanations on the following questions!
1. What are non-stationary and non-spherical wave effects?
2. What are the standards used in validating a massive MIMO based secure transmission scheme operating in TDD?
3. What determine the choice of a fading channel (Geometric based stochastic model or Correlation based stochastic model) and what kind of analysis is one expected to do if you choose either of the two?
4. What are the examples of each of the fading channels in (3)?
1. The term “non-stationary” can refer to different properties: signal can be non-stationary in time, frequency, space. In Massive MIMO, it is sometimes used to describe that a large array might observe signals with different strengths at different antennas – a type of spatial non-stationarity.
The transmitted waves are generally spherical. But if a receiving antenna array is the far-field of the transmitter, the income wave can be approximated as a plane (non-spherical) wave.
2. I am not aware of any standards for secure Massive MIMO transmission.
3. A geometry based model can be used to study signal propagation in a practical deployment area, but the results might not apply to other areas. A correlation based model can be used to study signal propagation in randomly generated areas. It gives a sense of how the performance varies over different areas, but one cannot connect it to a particular practical deployment area.
4. I don’t know which equation you are referring to.
Re: Question 4: I mean examples of (1) correlation based fading models and (2) Examples of geometric based fading models for both 2D and 3D models. I need examples of the fading models if the each above category.
2) Please do massive eavesdroppers exist in reality? If yes I need an example!
These channel models are described in my book Massive MIMO Networks (https://massivemimobook.com), Section 7.3.
I am not aware of any massive eavesdroppers in reality.
For the purpose of validating ones result, especially when secrecy techniques are implemented on mMIMO channels, are there any theoretical performances or targets which we can use to compare our performances?
I think you should try to use the same performance metrics as in non-mMIMO systems. It can for example be the secrecy capacity. I am not working on this topic myself so I don’t have any specific suggestions.
Can you please throw more light on non-orthogonal pilot signals and orthogonal pilot signals, because I am getting confused by it.
Good day prof. My question goes like this if Black = 100 kHz and Tc = 5 ms, then data samples = 500. So how many symbols is in 500 samples? Assuming I use QPSK modulation!
The following words mean the same thing in this context:
Samples = symbols = channel uses
So 500 QPSK modulation symbols in a coherence block.
Sir, when we says one OFDM symbol, what does it mean?
This blog post is not about OFDM symbols, but when you transmit using orthogonal frequency division multiplexing (OFDM), the transmission is divided into symbols that transmitted one at a time. Here is a quite good description: https://home.zhaw.ch/kunr/NTM1/literatur/LTE%20in%20a%20Nutshell%20-%20Physical%20Layer.pdf
Hello sir,
I’m a student doing a project related to pilot contamination. I wonder if we before pilot sequence transmission can we use another coherence block where a unique identification is given to the cell so that pilot contamination is reduced. Is it practically possible?
No, I don’t think this is possible. The channel changes between coherence blocks (by definition) so you cannot use information from one block to improve the next one. Maybe I just don’t understand what you are trying to do.
Sir, what I’m trying to say is, if we consider two base stations are present, even though two cells having same pilots, if their identification number are different, the same pilot from other cell arrives differently since the identification number is different. Here identification number is unique number given to cell. Can this be used to reduced pilot contamination? Is it possible at least in theory?
I don’t think this is possible. The cell identification number is not encoded into the pilot signals, and if they are, then the pilots are not the same anymore.
If I were you, I would start with modeling the system mathematically and thereby understanding what will happen.
Dear Sir,
I am doing thesis on massive MIMO pilot contamination reduction. I need some simulation codes such as pilot reuse, pilot scheduling, pilot pollution etc. If you have some codes of them, please send it to me. Thanks in advance.!
You can find a lot of code at my GitHub: https://github.com/emilbjornson?tab=repositories
Particularly my book Massive MIMO Networks contains a lot of simulation examples. If you use it in your thesis, you need to declare what you are utilizing in your thesis. Remember that it is often easier to implement something yourself, so you know how it works, than to learn someone else’s code and then add new portions to it.
How are pilot signals generated? And what is inter cell interference? And what is the relation between them?
Pilot signal is a predefined signal that both the transmitter and receiver know. When it is transmitted, the receiver can determine how it was distorted and thereby estimate the channel coefficients.
When the same pilot signal is transmitted in multiple cells at the same time, they will interfere with each other. This is what we call pilot contamination.
Good day sir, I am working on a thesis regarding the performance improvement for cell edge users in a cellular network. I had read this paper sir “Cooperative Multicell Precoding: Rate Region Characterization and Distributed Strategies With Instantaneous and Statistical CSI”. I am having difficulty in framing the equations in MATLAB. Could you please send me the simulation code for this paper? Thanks in advance!
Thank you for the interest in my paper!
This was one of the first papers that I wrote during my time as PhD student, before I knew what “research reproducibility” is. The code wasn’t prepared for being published and I don’t have it anymore.
You can find all of my published simulation code on GitHub: https://github.com/emilbjornson?tab=repositories