Sometime last week, the paper “Massive MIMO in the UL/DL of Cellular Networks: How Many Antennas Do We Need?” that I have co-authored reached 1000 citations (according to Google Scholar). I feel that this is a good moment to share some reflections on this work and discuss some conclusions we too hastily drew. The paper is an extension of a conference paper that appeared at the 2011 Allerton Conference. At that time, we could by no means anticipate the impact Massive MIMO would have and many people were quite doubtful about the technology (including myself). I still remember very well a heated discussion with an esteemed Bell Lab’s colleague trying to convince me that there were never ever going to be more than two active RF inputs into a base station!
Looking back, I am always wondering where the term “Massive MIMO” actually comes from. When we wrote our paper, the terms “large-scale antenna systems (LSAS)” or simply “large-scale MIMO” were commonly used to refer to base stations with very large antenna arrays, and I do not recall what made us choose our title.
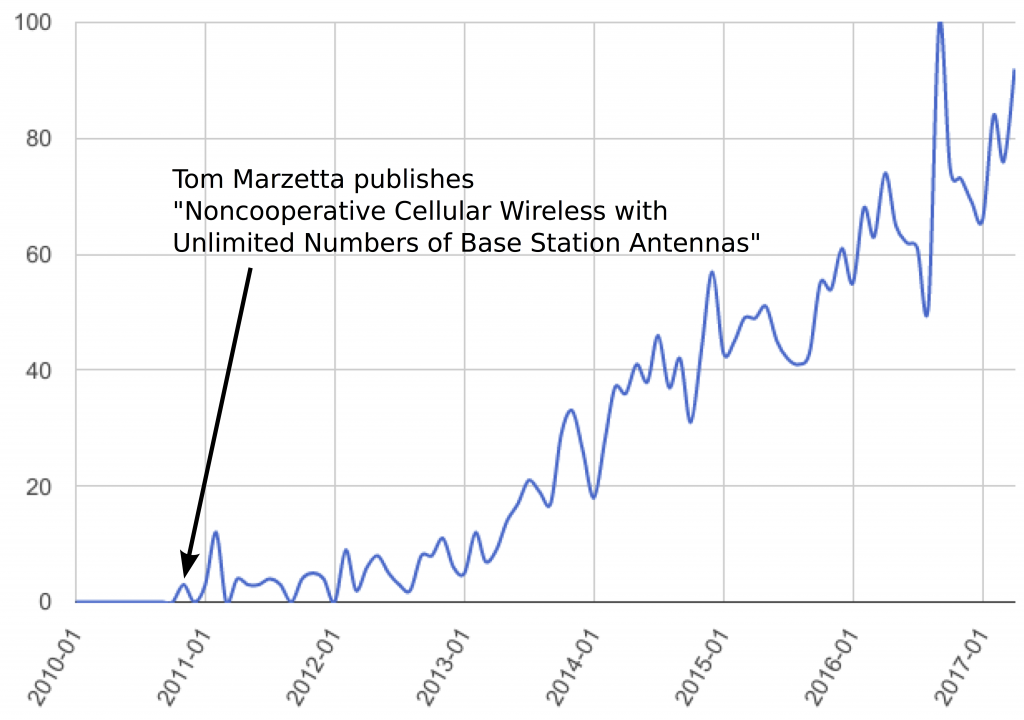
The Google Trends Chart for “Massive MIMO” above clearly shows that interest in this topic started roughly at the time Tom Marzetta’s seminal paper was published, although the term itself does not appear in it at all. If anyone has an idea or reference where the term “Massive MIMO” was first used, please feel free to write this in the comment field.
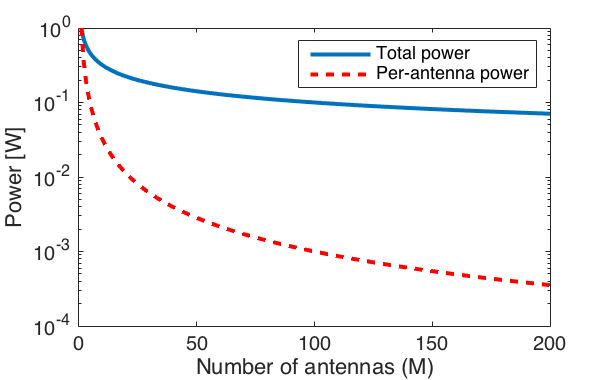
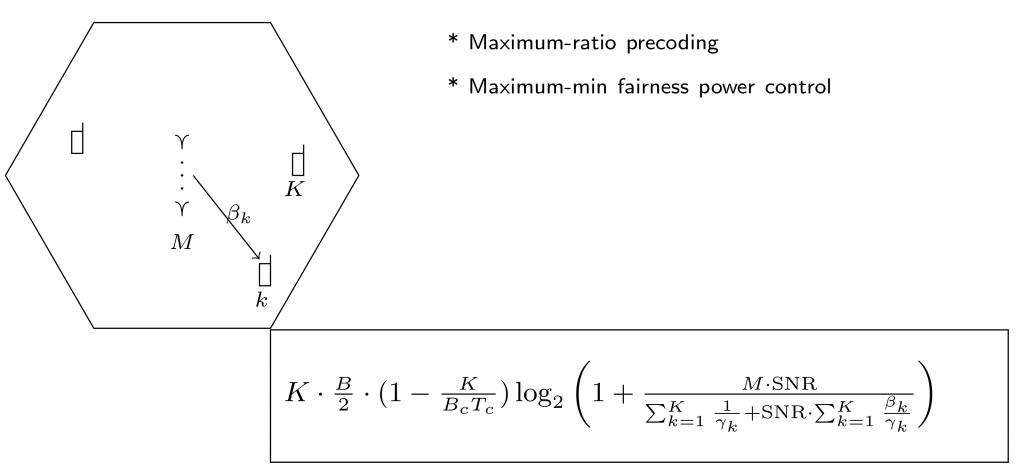
In case you have not read our paper, let me first explain the key question it tries to answer. Marzetta showed in his paper that the simplest form of linear receive combining and transmit precoding, namely maximum ratio combining (MRC) and transmission (MRT), respectively, achieve an asymptotic spectral efficiency (when the number of antennas goes to infinity) that is only limited by coherent interference caused by user equipments (UEs) using the same pilot sequences for channel training (see the previous blog post on pilot contamination). All non-coherent interference such as noise, channel gain uncertainty due to estimation errors, and interference magically vanishes thanks to the strong law of large numbers and favorable propagation. Intrigued by this beautiful result, we wanted to know what happens for a large but finite number of antennas 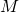 . Clearly, MRC/MRT are not optimal in this regime, and we wanted to quantify how much can be gained by using more advanced combining/precoding schemes. In other words, our goal was to figure out how many antennas could be “saved” by computing a matrix inverse, which is the key ingredient of the more sophisticated schemes, such as MMSE combining or regularized zero-forcing (RZF) precoding. Moreover, we wanted to compute how much of the asymptotic spectral efficiency can be achieved with
. Clearly, MRC/MRT are not optimal in this regime, and we wanted to quantify how much can be gained by using more advanced combining/precoding schemes. In other words, our goal was to figure out how many antennas could be “saved” by computing a matrix inverse, which is the key ingredient of the more sophisticated schemes, such as MMSE combining or regularized zero-forcing (RZF) precoding. Moreover, we wanted to compute how much of the asymptotic spectral efficiency can be achieved with 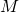 antennas. Please read our paper if you are interested in our findings.
antennas. Please read our paper if you are interested in our findings.
What is interesting to notice is that we (and many other researchers) had always taken the following facts about Massive MIMO for granted and repeated them in numerous papers without further questioning:
- Due to pilot contamination, Massive MIMO has a finite asymptotic capacity
- MRC/MRT are asymptotically optimal
- More sophisticated receive combining and transmit precoding schemes can only improve the performance for finite
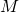
We have recently uploaded a new paper on Arxiv which proves that all of these “facts” are incorrect and essentially artifacts from using simplistic channel models and suboptimal precoding/combining schemes. What I find particularly amusing is that we have come to this result by carefully analyzing the asymptotic performance of the multicell MMSE receive combiner that I mentioned but rejected in the 2011 Allerton paper. To understand the difference between the widely used single-cell MMSE (S-MMSE) combining and the (not widely used) multicell MMSE (M-MMSE) combining, let us look at their respective definitions for a base station located in cell 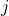 :
:
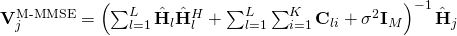
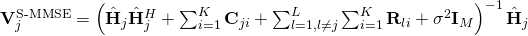
where 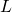 and
and 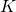 denote the number of cells and UEs per cell,
denote the number of cells and UEs per cell, 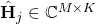 is the estimated channel matrix from the UEs in cell
is the estimated channel matrix from the UEs in cell 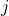 , and
, and 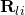 and
and 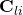 are the covariance matrices of the channel and the channel estimation errors of UE
are the covariance matrices of the channel and the channel estimation errors of UE 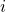 in cell
in cell 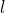 , respectively. While M-MMSE combining uses estimates of the channels from all UEs in all cells, the simpler S-MMSE combining uses only channel estimates from the UEs in the own cell. Importantly, we show that Massive MIMO with M-MMSE combining has unlimited capacity while Massive MIMO with S-MMSE combining has not! This behavior is shown in the following figure:
, respectively. While M-MMSE combining uses estimates of the channels from all UEs in all cells, the simpler S-MMSE combining uses only channel estimates from the UEs in the own cell. Importantly, we show that Massive MIMO with M-MMSE combining has unlimited capacity while Massive MIMO with S-MMSE combining has not! This behavior is shown in the following figure:
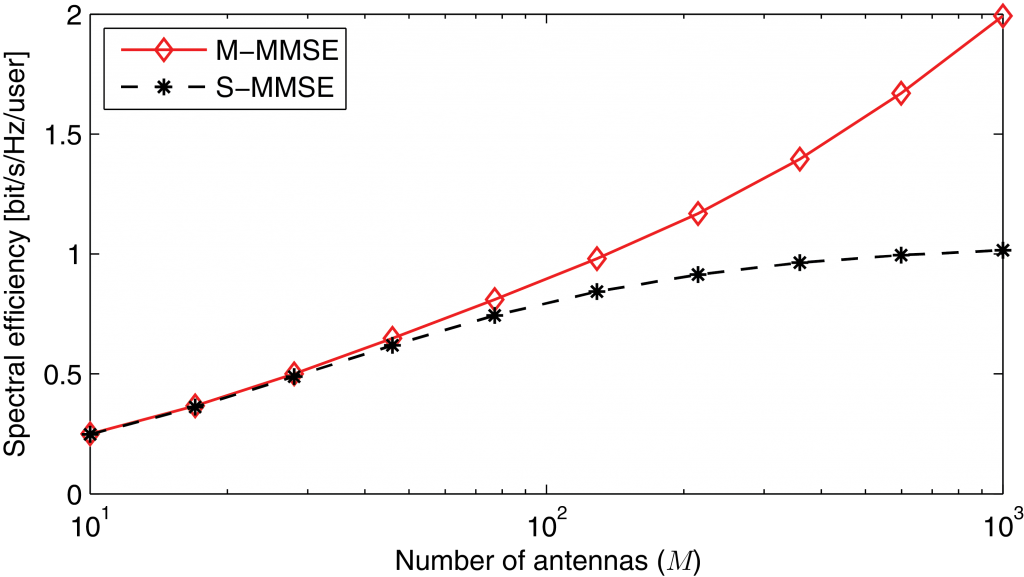
In the light of this new result, I wish that we would not have made the following remark in our 2011 Allerton paper:
“Note that a BS could theoretically estimate
all channel matrices 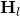 (…) to further
(…) to further
improve the performance. Nevertheless, high path loss to
neighboring cells is likely to render these channel estimates unreliable and the potential performance gains are expected to be marginal.”
We could not have been more wrong about it!
In summary, although we did not understand the importance of M-MMSE combining in 2011, I believe that we were asking the right questions. In particular, the consideration of individual channel covariance matrices for each UE has been an important step for the analysis of Massive MIMO systems. A key lesson that I have learned from this story for my own research is that one should always question fundamental assumptions and wisdom.