I have been wondering for years if “MIMO” will always be a term exclusively used by engineers and a few well-informed consumers, or if it eventually becomes a word that most people are using. Will you ever hear kids saying: “I want a MIMO tablet for Christmas”?
I have been think that it can go either way – it is in the hands of marketing people. Advanced Wifi routers have been marketed with MIMO functionality for some years, but the impact is limited since most people get their routers as part of their internet subscriptions instead of buying them separately. Hence, the main question is: will handset manufactures and telecom operators start using the MIMO term when marketing products to end customers?
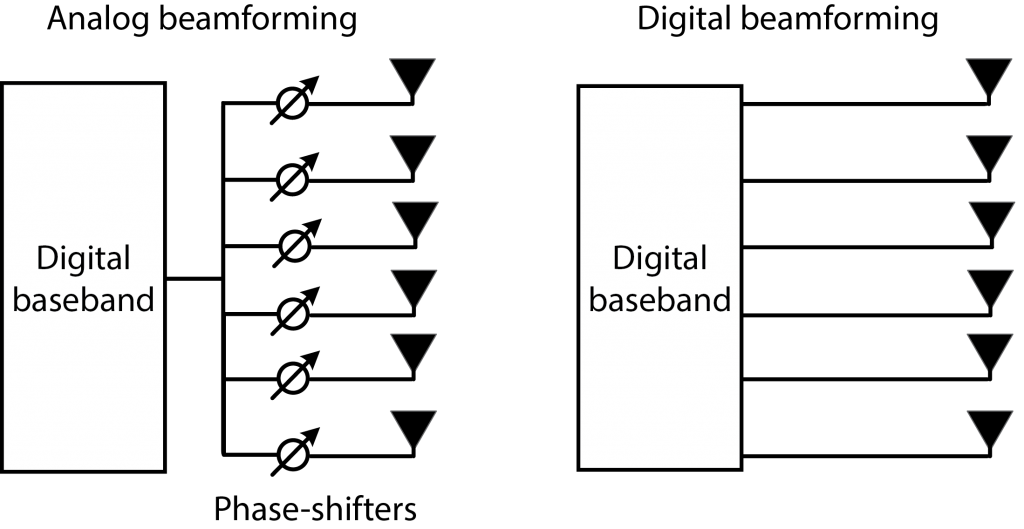
Maybe we have the answer because Sprint, an American telecom operator, is currently marketing their 2018 deployment of new LTE technology by talking publicly about “Massive MIMO”. As I wrote back in March, Sprint and Ericsson were to conduct field tests in the second half of 2017. Results from the tests conducted in Seattle, Washington and Plano, Texas, have now been described in a press release. The tests were carried at a carrier frequency in the 2.5 GHz band using TDD mode and an Ericsson base station with 64 transmit/receive antennas. It is fair to call this Massive MIMO, although 64 antennas is in the lower end of the interval that I would call “massive”.
The press release describes “peak speeds of more than 300 Mbps using a single 20 MHz channel”, which corresponds to a spectral efficiency of 15 bit/s/Hz. That is certainly higher than you can get in legacy LTE networks, but it is less than some previous field tests.
Hence, when the Sprint COO of Technology, Guenther Ottendorfer, describes their Massive MIMO deployment with the words “You ain’t seen nothing yet”, I hope that this means that we will see network deployments with substantially higher spectral efficiencies than 15 bit/s/Hz in the years to come.
Several videos about the field test in Seattle have recently appeared. The first one demonstrates that 100 people can simultaneously download a video, which is not possible in legacy networks. Since the base station has 64 antennas, the 100 users are probably served by a combination of spatial multiplexing and conventional orthogonal time-frequency multiplexing.
The second video provides some more technical details about the setup used in the field test.