What is Massive MIMO?  The term has been used for many different systems and the only common denominator seems to be a multi-user MIMO system with everything between 10 to infinitely many antennas.  In the book [1], the authors give the following definition:

“Massive MIMO is a useful and scalable version of Multiuser MIMO.  There are three fundamental distinctions between Massive MIMO and conventional Multiuser MIMO. First, only the base station learns G. Second, M is typically much larger than K, although this does not have to be the case. Third, simple linear signal processing is used both on the uplink and on the downlink. These features render Massive MIMO scalable with respect to the number of base station antennas, M.”

(Note: M is the number of antennas, K is the number of users, and G denotes the channel matrix).

In [2], we find another definition:

“Massive MIMO is a multi-user MIMO system with M antennas and K users per BS. The system is characterized by M ≫ K and operates in TDD mode using linear uplink and downlink processing.”

Both are nice general definitions that cover most systems that commonly are called “Massive MIMO”.  However, their generality also makes them vague and they fail to pinpoint the essence of Massive MIMO.  Here, is my take on a slightly more precise definition:

“Massive MIMO is a multi-user MIMO system that (1) serves multiple users through spatial multiplexing over a channel with favorable propagation in time-division duplex and (2) relies on channel reciprocity and uplink pilots to obtain channel state information.”

Now, you might ask: So what is then “favorable propagation”?  We need a second definition:

“The propagation is said to be favorable when users are mutually orthogonal in some practical sense.”

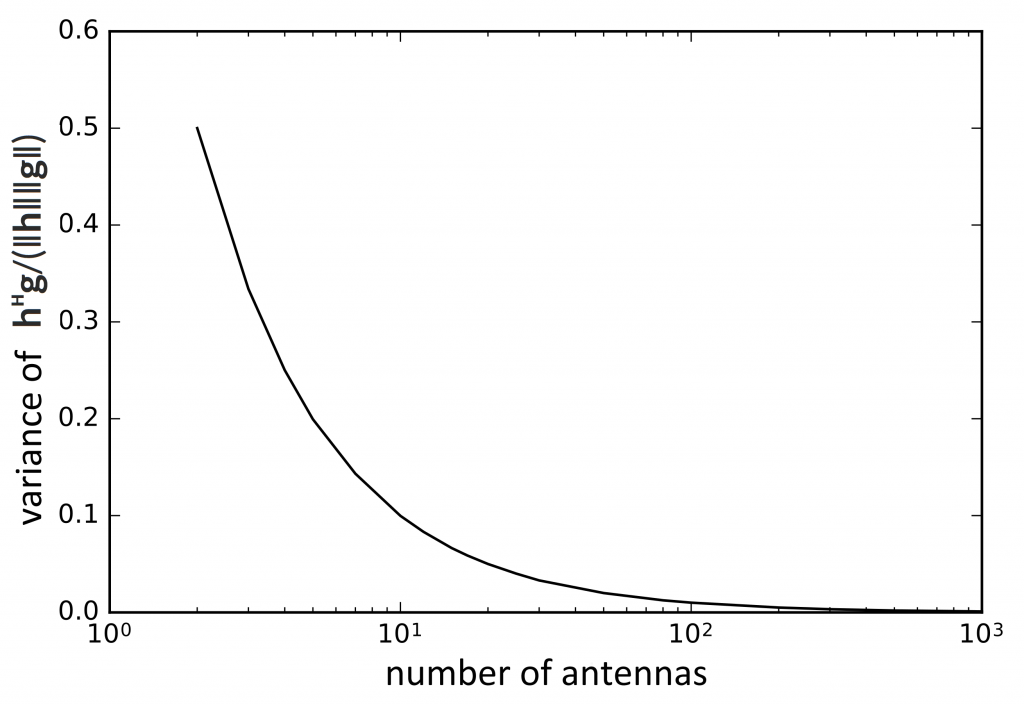
Again you ask: in what practical sense?  If h∈ℂᴹ is the channel vector to one user and g∈ℂᴹ the channel vector to another, the users are said to be orthogonal if hᴴg = 0.  Unfortunately, this is never true in a real system.  It can be practically true, however, if we say that users are practically orthogonal when hᴴg/(‖h‖‖g‖) has mean zero and a variance that is much smaller than one.

There we go: a more-or-less rigorous definition of Massive MIMO.  Note that this definition does not require the number of users to be small in any sense.  So, to the big question: How many antennas does a base station need to be “massive”? The answer is given for the i.i.d. Rayleigh fading channel in the following curve that shows how the users’ channels become practically orthogonal as the number of antennas is increased.

1. [1] T. L. Marzetta, E. G. Larsson, H. Yang, N. Q. Ngo. Fundamentals of Massive MIMO. Cambridge University Press, 2016.
2. [2] T. V. Chien, E. Björnson, “Massive MIMO Communications,” in 5G Mobile Communications, W. Xiang et al. (eds.), pp. 77-116, Springer, 2017.