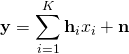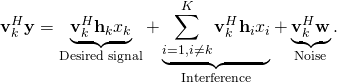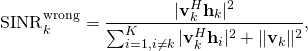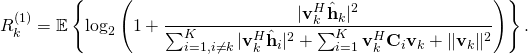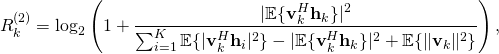We are used to measuring performance in terms of the signal-to-interference-and-noise ratio (SINR), but this is seldom the actual performance metric in communication systems. In practice, we might be interested in a function of the SINR, such as the data rate (a.k.a. spectral efficiency), bit-error-rate, or mean-squared error in the data detection. When the receiver has perfect channel state information (CSI), the aforementioned metrics are all functions of the same SINR expression, where the power of the received signal is divided by the power of the interference plus noise. Details can be found in Examples 1.6-1.8 of the book Optimal Resource Allocation in Coordinated Multi-Cell Systems.
 In most cases, the receiver only has imperfect CSI and then it is harder to measure the performance. In fact, it took me years to understand this properly. To explain the complications, consider the uplink of a single-cell Massive MIMO system with
In most cases, the receiver only has imperfect CSI and then it is harder to measure the performance. In fact, it took me years to understand this properly. To explain the complications, consider the uplink of a single-cell Massive MIMO system with 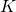 single-antenna users and
single-antenna users and 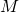 antennas at the base station. The received
antennas at the base station. The received 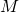 -dimensional signal is
-dimensional signal is
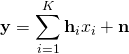
where 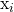 is the unit-power information signal from user
is the unit-power information signal from user 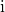 ,
, 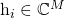 is the fading channel from this user, and
is the fading channel from this user, and 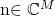 is unit-power additive Gaussian noise. In general, the base station will only have access to an imperfect estimate
is unit-power additive Gaussian noise. In general, the base station will only have access to an imperfect estimate 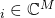 of
of 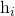 , for
, for 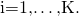
Suppose the base station uses 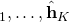 to select a receive combining vector
to select a receive combining vector 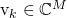 for user
for user 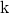 . The base station then multiplies it with
. The base station then multiplies it with 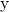 to form a scalar that is supposed to resemble the information signal
to form a scalar that is supposed to resemble the information signal 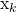 :
:
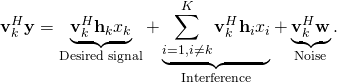
From this expression, a common mistake is to directly say that the SINR is
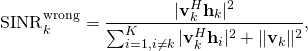
which is obtained by computing the power of each of the terms (averaged over the signal and noise), and then claim that 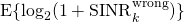 is an achievable rate (where the expectation is with respect to the random channels). You can find this type of arguments in many papers, without proof of the information-theoretic achievability of this rate value. Clearly,
is an achievable rate (where the expectation is with respect to the random channels). You can find this type of arguments in many papers, without proof of the information-theoretic achievability of this rate value. Clearly, 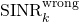 is an SINR, in the sense that the numerator contains the total signal power and the denominator contains the interference power plus noise power. However, this doesn’t mean that you can plug
is an SINR, in the sense that the numerator contains the total signal power and the denominator contains the interference power plus noise power. However, this doesn’t mean that you can plug 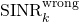 into “Shannon’s capacity formula” and get something sensible. This will only yield a correct result when the receiver has perfect CSI.
into “Shannon’s capacity formula” and get something sensible. This will only yield a correct result when the receiver has perfect CSI.
A basic (but non-conclusive) test of the correctness of a rate expression is to check that the receiver can compute the expression based on its available information (i.e., estimates of random variables and deterministic quantities). Any expression containing 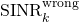 fails this basic test since you need to know the exact channel realizations
fails this basic test since you need to know the exact channel realizations 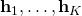 to compute it, although the receiver only has access to the estimates.
to compute it, although the receiver only has access to the estimates.
What is the right approach?
Remember that the SINR is not important by itself, but we should start from the performance metric of interest and then we might eventually interpret a part of the expression as an effective SINR. In Massive MIMO, we are usually interested in the ergodic capacity. Since the exact capacity is unknown, we look for rigorous lower bounds on the capacity. There are several bounding techniques to choose between, whereof I will describe the two most common ones.
The first lower bound on the uplink capacity can be applied when the channels are Gaussian distributed and 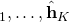 are the MMSE estimates with the corresponding estimation error covariance matrices
are the MMSE estimates with the corresponding estimation error covariance matrices 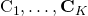 . The ergodic capacity of user
. The ergodic capacity of user 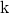 is then lower bounded by
is then lower bounded by
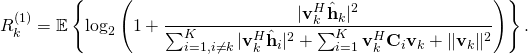
Note that this expression can be computed at the receiver using only the available channel estimates (and deterministic quantities). The ratio inside the logarithm can be interpreted as an effective SINR, in the sense that the rate is equivalent to that of a fading channel where the receiver has perfect CSI and an SNR equal to this effective SINR. A key difference from 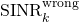 is that only the part of the desired signal that is received along the estimated channel appears in the numerator of the SINR, while the rest of the desired signal appears as
is that only the part of the desired signal that is received along the estimated channel appears in the numerator of the SINR, while the rest of the desired signal appears as 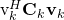 in the denominator. This is the price to pay for having imperfect CSI at the receiver, according to this capacity bound, which has been used by Hoydis et al. and Ngo et al., among others.
in the denominator. This is the price to pay for having imperfect CSI at the receiver, according to this capacity bound, which has been used by Hoydis et al. and Ngo et al., among others.
The second lower bound on the uplink capacity is
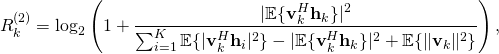
which can be applied for any channel fading distribution. This bound provides a value close to 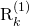 when there is substantial channel hardening in the system, while
when there is substantial channel hardening in the system, while 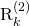 will greatly underestimate the capacity when
will greatly underestimate the capacity when 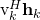 varies a lot between channel realizations. The reason is that to obtain this bound, the receiver detects the signal as if it is received over a non-fading channel with gain
varies a lot between channel realizations. The reason is that to obtain this bound, the receiver detects the signal as if it is received over a non-fading channel with gain 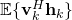 (which is deterministic and thus known in theory, and easy to measure in practice), but there are no approximations involved so
(which is deterministic and thus known in theory, and easy to measure in practice), but there are no approximations involved so 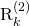 is always a valid bound.
is always a valid bound.
Since all the terms in 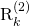 are deterministic, the receiver can clearly compute it using its available information. The main merit of
are deterministic, the receiver can clearly compute it using its available information. The main merit of 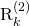 is that the expectations in the numerator and denominator can sometimes be computed in closed form; for example, when using maximum-ratio and zero-forcing combining with i.i.d. Rayleigh fading channels or maximum-ratio combining with correlated Rayleigh fading. Two early works that used this bound are by Marzetta and by Jose et al..
is that the expectations in the numerator and denominator can sometimes be computed in closed form; for example, when using maximum-ratio and zero-forcing combining with i.i.d. Rayleigh fading channels or maximum-ratio combining with correlated Rayleigh fading. Two early works that used this bound are by Marzetta and by Jose et al..
The two uplink rate expressions can be proved using capacity bounding techniques that have been floating around in the literature for more than a decade; the main principle for computing capacity bounds for the case when the receiver has imperfect CSI is found in a paper by Medard from 2000. The first concise description of both bounds (including all the necessary conditions for using them) is found in Fundamentals of Massive MIMO. The expressions that are presented above can be found in Section 4 of the new book Massive MIMO Networks. In these two books, you can also find the right ways to compute rigorous lower bounds on the downlink capacity in Massive MIMO.
In conclusion, to avoid mistakes, always start with rigorously computing the performance metric of interest. If you are interested in the ergodic capacity, then you start from one of the canonical capacity bounds in the above-mentioned books and verify that all the required conditions are satisfied. Then you may interpret part of the expression as an SINR.

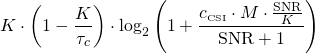
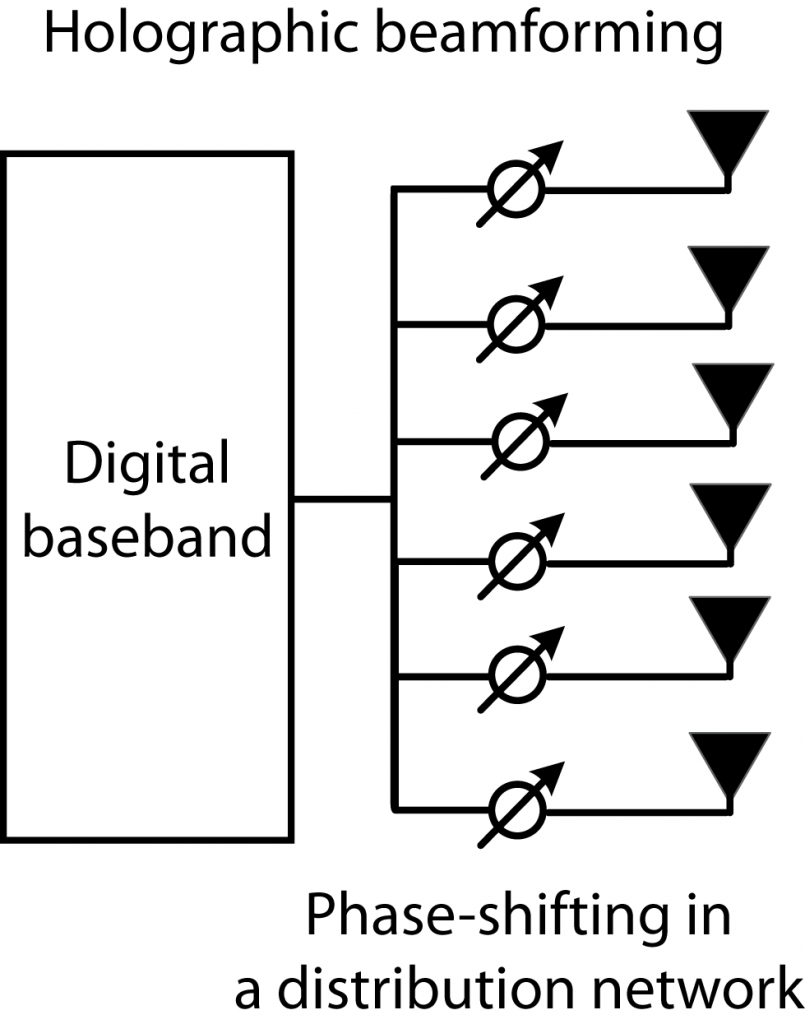 Will the futuristic-sounding holographic beamforming make Massive MIMO obsolete? Not at all, because this is a new implementation architecture, not a new beamforming scheme or spatial multiplexing method. According to the
Will the futuristic-sounding holographic beamforming make Massive MIMO obsolete? Not at all, because this is a new implementation architecture, not a new beamforming scheme or spatial multiplexing method. According to the 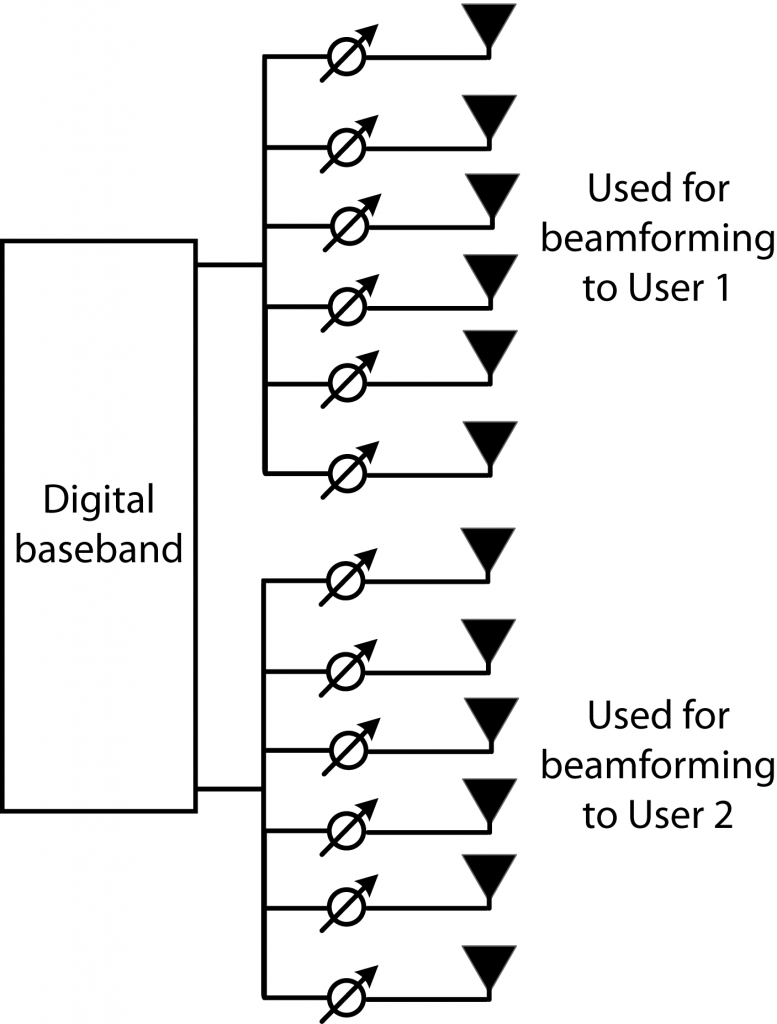
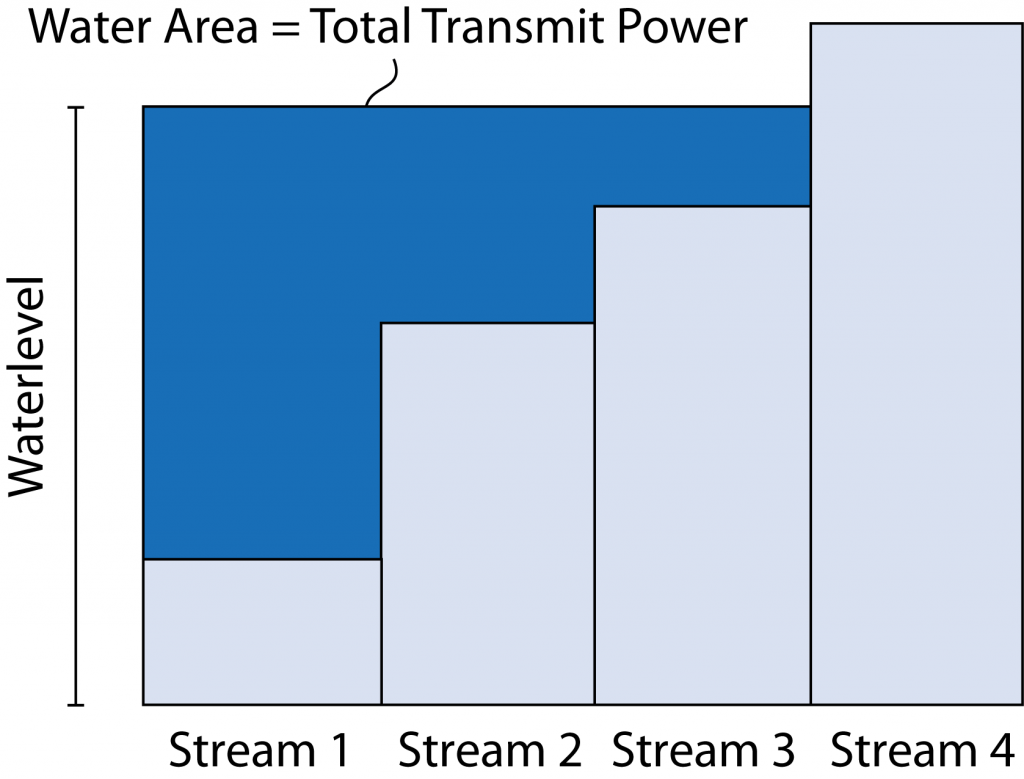
 In most cases, the receiver only has imperfect CSI and then it is harder to measure the performance. In fact, it took me years to understand this properly. To explain the complications, consider the uplink of a single-cell Massive MIMO system with
In most cases, the receiver only has imperfect CSI and then it is harder to measure the performance. In fact, it took me years to understand this properly. To explain the complications, consider the uplink of a single-cell Massive MIMO system with