The transmitted signal ![]() from an
from an ![]() -antenna base station can consist of multiple information signals that are transmitted using different precoding (e.g., different spatial directivity). When there are
-antenna base station can consist of multiple information signals that are transmitted using different precoding (e.g., different spatial directivity). When there are ![]() unit-power data signals
unit-power data signals ![]() intended for
intended for ![]() different users, the transmitted signal can be expressed as
different users, the transmitted signal can be expressed as
(1) 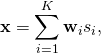
where ![]() are the
are the ![]() -dimensional precoding vectors assigned to the different users. The direction of the vector
-dimensional precoding vectors assigned to the different users. The direction of the vector ![]() determines the spatial directivity of the signal
determines the spatial directivity of the signal ![]() , while the squared norm
, while the squared norm ![]() determines the associated transmit power. Massive MIMO usually means that
determines the associated transmit power. Massive MIMO usually means that ![]() .
.
When selecting the precoding vectors, we need to make sure that we are not using too much transmit power. If the maximum power is ![]() and we define the
and we define the ![]() precoding matrix
precoding matrix
(2) ![]()
then we need to make sure that the squared Frobenius norm of ![]() equals the maximum transmit power:
equals the maximum transmit power:
(3) ![]()
In the Massive MIMO literature, there are two popular methods to achieve that: matrix normalization and vector normalization. The papers [Ref1], [Ref2] consider both methods, while other papers only consider one of the methods. The main idea is to start from an arbitrarily selected precoding matrix ![]() and then adapt it to satisfy the power constraint in (3).
and then adapt it to satisfy the power constraint in (3).
Matrix normalization: In this case, we take the matrix ![]() and scales all the entries with the same number, which is selected to satisfy (3). More precisely, we select
and scales all the entries with the same number, which is selected to satisfy (3). More precisely, we select
(4) ![]()
Vector normalization: In this case, we first normalize each column in ![]() to have unit norm and then scale them all with
to have unit norm and then scale them all with ![]() to satisfy (3). More precisely, we select
to satisfy (3). More precisely, we select
(5) ![]()
Which of the two normalizations should be used?
This is a question that I receive now and then, so I wrote this blog post to answer it once and for all. My answer: none of them!
The problem with matrix normalization is that the method that was used to select ![]() will determine how the transmit power is allocated between the different signals/users. Hence, we are not in control of the power allocation and we cannot fairly compare different precoding schemes. For example, maximum-ratio (MR) allocates more power to users with strong channels than users with weak channels, while zero-forcing (ZF) does the opposite. Hence, if one tries to compare MR and ZF under matrix normalization, the different power allocations will strongly influence the results.
will determine how the transmit power is allocated between the different signals/users. Hence, we are not in control of the power allocation and we cannot fairly compare different precoding schemes. For example, maximum-ratio (MR) allocates more power to users with strong channels than users with weak channels, while zero-forcing (ZF) does the opposite. Hence, if one tries to compare MR and ZF under matrix normalization, the different power allocations will strongly influence the results.
This issue is resolved by vector normalization. However, the problem with vector normalization is that all users are assigned the same amount of power, which is undesirable if some users have strong channels and others have weak channels. One should always make a conscious decision when it comes to power allocation between users.
What we should do instead is to select the precoding matrix as
(6) ![]()
where ![]() are variables representing the power assigned to each of the users. These should be carefully selected to maximize some performance goals of the network, such as the sum rate, proportional fairness, or max-min fairness. In any case, the power allocation must be selected to satisfy the constraint
are variables representing the power assigned to each of the users. These should be carefully selected to maximize some performance goals of the network, such as the sum rate, proportional fairness, or max-min fairness. In any case, the power allocation must be selected to satisfy the constraint
(7) 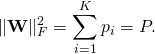
There are plenty of optimization algorithms that can be used for this purpose. You can find further details, examples, and references in Section 7.1 of my book Massive MIMO networks.