Several people have recently asked me for a simple way to quantify the spectral efficiency gains that we can expect from Massive MIMO. In theory, going from 4 to 64 antennas is just a matter of changing a parameter value. However, many practical issues need be solved to bring the technology into reality and the solutions might only be developed if we can convince ourselves that the gains are sufficiently large.
While there is no theoretical upper limit on how spectrally efficient Massive MIMO can become when adding more antennas, we need to set some reasonable first goals. Currently, many companies are trying to implement analog beamforming in a cost-efficient manner. That will allow for narrow beamforming, but not spatial multiplexing.
By following the methodology in Section 3.3.3 in Fundamentals of Massive MIMO, a simple formula for the downlink spectral efficiency is:
(1) 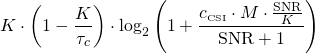
where ![]() is the number of base-station antennas,
is the number of base-station antennas, ![]() is the number of spatially multiplexed users,
is the number of spatially multiplexed users, ![]() is the quality of the channel estimates, and
is the quality of the channel estimates, and ![]() is the number of channel uses per channel coherence block. For simplicity, I have assumed the same pathloss for all the users. The variable
is the number of channel uses per channel coherence block. For simplicity, I have assumed the same pathloss for all the users. The variable ![]() is the nominal signal-to-noise ratio (SNR) of a user, achieved when
is the nominal signal-to-noise ratio (SNR) of a user, achieved when ![]() . Eq. (1) is a rigorous lower bound on the sum capacity, achieved under the assumptions of maximum ratio precoding, i.i.d. Rayleigh fading channels, and equal power allocation. With better processing schemes, one can achieve substantially higher performance.
. Eq. (1) is a rigorous lower bound on the sum capacity, achieved under the assumptions of maximum ratio precoding, i.i.d. Rayleigh fading channels, and equal power allocation. With better processing schemes, one can achieve substantially higher performance.
To get an even simpler formula, let us approximate (1) as
(2) ![]()
by assuming a large channel coherence and negligible noise.
What does the formula tell us?
If we increase ![]() while
while ![]() is fixed , we will observe a logarithmic improvement in spectral efficiency. This is what analog beamforming can achieve for
is fixed , we will observe a logarithmic improvement in spectral efficiency. This is what analog beamforming can achieve for ![]() and, hence, I am a bit concerned that the industry will be disappointed with the gains that they will obtain from such beamforming in 5G.
and, hence, I am a bit concerned that the industry will be disappointed with the gains that they will obtain from such beamforming in 5G.
If we instead increase ![]() and
and ![]() jointly, so that
jointly, so that ![]() stays constant, then the spectral efficiency will grow linearly with the number of users. Note that the same transmit power is divided between the
stays constant, then the spectral efficiency will grow linearly with the number of users. Note that the same transmit power is divided between the ![]() users, but the power-reduction per user is compensated by increasing the array gain
users, but the power-reduction per user is compensated by increasing the array gain ![]() so that the performance per user remains the same.
so that the performance per user remains the same.
The largest gains come from spatial multiplexing
To give some quantitative numbers, consider a baseline system with ![]() and
and ![]() that achieves 2 bit/s/Hz. If we increase the number of antennas to
that achieves 2 bit/s/Hz. If we increase the number of antennas to ![]() , the spectral efficiency will become 5.6 bit/s/Hz. This is the gain from beamforming. If we also increase the number of users to
, the spectral efficiency will become 5.6 bit/s/Hz. This is the gain from beamforming. If we also increase the number of users to ![]() users, we will get 32 bit/s/Hz. This is the gain from spatial multiplexing. Clearly, the largest gains come from spatial multiplexing and adding many antennas is a necessary way to facilitate such multiplexing.
users, we will get 32 bit/s/Hz. This is the gain from spatial multiplexing. Clearly, the largest gains come from spatial multiplexing and adding many antennas is a necessary way to facilitate such multiplexing.
This analysis has implicitly assumed full digital beamforming. An analog or hybrid beamforming approach may achieve most of the array gain for ![]() . However, although hybrid beamforming allows for spatial multiplexing, I believe that the gains will be substantially smaller than with full digital beamforming.
. However, although hybrid beamforming allows for spatial multiplexing, I believe that the gains will be substantially smaller than with full digital beamforming.

I wonder if it, for an adaptive antenna system, is easier to steer a null towards an interferer than increasing the gain towards the user? I.e. to increase the SINR, is it more efficient to block, null, out the interferer than to focus the power to the user.
Is there a limit for how many independent steerable nulls an adaptive N-antenna array can have?
It is much easier to focus the signal on the desired user than to create a null. When you are forming a null, you need the signal components from the different antennas to sum up to zero. When summing up terms that are large in magnitude but have different signs, a small error can make a huge difference.
However, if you want to increase the SINR, it is important to put nulls (or at least actively mitigate the interference, even if you don’t bring it down to zero).
With N antennas, you can create up to N nulls.
How important is accurate CSI, considering other properties such as the spatial domain and carrier frequency in the design?
The parameter that I called c_CSI lies in the interval [0,1] and represents the accuracy of the CSI. The scaling behavior is the same for any value of c_CSI, but it is certainly preferable to have a large value of c_CSI.
Thank you for this elaboration on the capacity, or spectrum efficiency, however there is one thing I need some clarifications about. I thought that in order to implement spatial multiplexing, full digital beamforming was needed, and it wouldn’t be possible with analogue beamforming because you have only one RF-chain and consequently share the antenna distribution network. So, it is not only substantially smaller, but not there at all. Or have I missed something?
I agree with you. I accidentally lumped analog and hybrid beamforming together in the last paragraph, but it is only with hybrid beamforming that you can actually do spatial multiplexing (of as many users as there are RF chains). I have rephrased that paragraph now.
What theoretical throughput gain can be expected for a repeater MiMo system in a vehicle/train, (2×2, 4×4, etc) when spatial multiplexing and polarisation of signals are implemented in telecom network?
When using a repeater, the channel capacity is basically the lowest of:
Link 1: the capacity from the base station to the repeater;
Link 2: the capacity from the repeater to the users.
I would guess that it is link 1 that is usually the limiting factor since the propagation distances are much longer than within the vehicle. Hence, the benefit of using MIMO would primarily be to gather more signal power over Link 1. When doubling the number of antennas, one can increase the signal-to-noise ratio by 3 dB. It is important to have dual polarization to not be subject to signal losses due to polarization mismatching.
I am a bit skeptical to using spatial multiplexing. I think that the channel will not be sufficiently rich for that, particularly not when considering trains that are moving in rather open environments.
Hello Emil,
I did have a look at chapter 3.3.3 in the book but wasn’t able to come up with a way of transforming that formula into yours.
How did you reach that formula for the spectral efficiency in (1)?
You can start from the SINR expression in (3.64) and set n_k = 1/K (equal power allocation). You then set SNR = rho_dl * beta_k (assuming beta_k is the same for all users, so it is a constant). gamma_k/beta_k is what I call c_CSI. Finally, you compute the sum rate using (3.74), with tau_p = K.
Hi Emil,
It is not completely related with this section but can you show me some references on how I can find the phase distribution of each received component with massive MIMO after beamforming? I would expect that with beamforming the phase of each received signal will be more aligned (not uniform) but I am not sure what the distribution will be and as the number of antenna increases, this alignment will increase as well I suppose.
Thank you,
Mehmet
Hi Mehmet,
You can have a look at (1.45) in my book Massive MIMO networks (https://massivemimobook.com). If w_0k is selected to be identical to h_0k^0, then the inner product gives a sum with positive real-valued terms. Hence, all the received components are phase-aligned. If w_0k is instead based on a noisy estimate of h_0k^0, then the components won’t be perfectly phase-aligned.
Thank you Professor for the blog. I have one query. Will the massive mimo antenna gain affect the maximum transmit power? For example, if the maximum transmits power for BS is 30 dBm according to license the operator have and antenna gain is 10 dBi by deploying massive mimo, which will result in the directive beams, does it mean that the maximum transmit power will be 30 – 10 = 20 dBm? If yes, how can quantify antenna gain in terms of number of antennas?
There are different things that can be specified in licenses. A maximum transmit power is one thing and the effective isotropic radiated power (EIRP) is another thing. The latter is computed by taking the maximum power and add the maximum array/antenna gain. The EIRP limits are higher than the limit on maximum power.
There are two parts of the answer to your question: Yes, if you keep adding more antennas to the base station, the license will eventually force you to reduce the transmit power to satisfy the EIRP limits. However, existing base stations are already using directive antennas, but with a fixed directivity of 15-20 dBi. The main feature of Massive MIMO is that you can steer the directivity, while the maximum array gain of current Massive MIMO base stations are also in the 15-20 dBi range.
Hi professor,
Can we do spatial multiplexing at the user equipment (UE)?
Yes, a UE can transmit/receive multiple streams of data that are transmitted using different spatial directivity. This is called “layers” in 3GPP.
Sir can you please provide good references for layers in 3GPP
Erik Dahlman, Stefan Parkvall, Johan Sköld, “5G NR: The Next Generation Wireless Access Technology” Academic Press 2018.
Dear Emil,
Your posts are excellent!
I have a question related with quantization of the channel (CSI).
In your approach, you define c_ CSI in [0,1] as the quality of the channel estimate.
If we assume, that our system have a limited feedback to report the channel CSI ( Users to BS). It means that the precoding is calculated with an approximation of b bits of the real channel. Can we employ a parameter similar to c_ CSI to model this effect? Do you have a reference about that?
Thank you for your work!
A classical reference is “MIMO broadcast channels with finite-rate feedback” but it doesn’t contain a formula of the indicated kind. I’m not sure if one can find derive such a formula. A main issue is that c_CSI will be a function of both the b bits and the number of antennas M, since the feedback load increases with the number of antennas.
Thank you!
Your post is very useful for us!
I found this digest of massive MIMO. Thanks Emil!!!