It is often claimed in the academic literature that Massive MIMO can greatly improve the spectral efficiency. What does it mean, qualitatively and quantitatively? This is what I will try to explain.
With spectral efficiency, we usually mean the sum spectral efficiency of the transmissions in a cell of a cellular network. It is measured in bit/s/Hz. If you multiply it with the bandwidth, you will get the cell throughput measured in bit/s. Since the bandwidth is a scarce resource, particularly at the frequencies below 5 GHz that are suitable for network coverage, it is highly desirable to improve the cell throughput by increasing the spectral efficiency rather than increasing the bandwidth.
A great way to improve the spectral efficiency is to simultaneously serve many user terminals in the cell, over the same bandwidth, by means of space division multiple access. This is where Massive MIMO is king. There is no doubt that this technology can improve the spectral efficiency. The question is rather “how much?”
Earlier this year, the joint experimental effort by the universities in Bristol and Lund demonstrated an impressive spectral efficiency of 145.6 bit/s/Hz, over a 20 MHz bandwidth in the 3.5 GHz band. The experiment was carried out in a single-cell indoor environment. Their huge spectral efficiency can be compared with 3 bit/s/Hz, which is the IMT Advanced requirement for 4G. The remarkable Massive MIMO gain was achieved by spatial multiplexing of data signals to 22 users using 256-QAM. The raw spectral efficiency is 176 bit/s/Hz, but 17% was lost for practical reasons. You can read more about this measurement campaign here:
http://www.bristol.ac.uk/news/2016/may/5g-wireless-spectrum-efficiency.html
256-QAM is generally not an option in cellular networks, due to the inter-cell interference and unfavorable cell edge conditions. Numerical simulations can, however, predict the practically achievable spectral efficiency. The figure below shows the uplink spectral efficiency for a base station with 200 antennas that serves a varying number of users. Interference from many tiers of neighboring cells is considered. Zero-forcing detection, pilot-based channel estimation, and power control that gives every user 0 dB SNR are assumed. Different curves are shown for different values of τc, which is the number of symbols per channel coherence interval. The curves have several peaks, since the results are optimized over different pilot reuse factors.
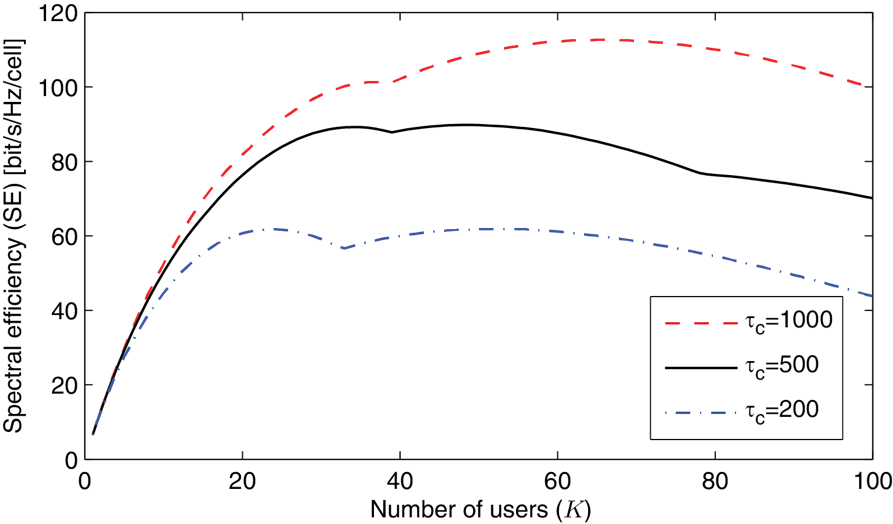
From this simulation figure we observe that the spectral efficiency grows linearly with the number of users, for the first 30-40 users. For larger user numbers, the spectral efficiency saturates due to interference and limited channel coherence. The top value of each curve is in the range from 60 to 110 bit/s/Hz, which are remarkable improvements over the 3 bit/s/Hz of IMT Advanced.
In conclusion, 20x-40x improvements in spectral efficiency over IMT Advanced are what to expect from Massive MIMO.

I note that optimum, sometimes, is to serve up to K = 70 users with M = 200 base station antennas. It is thus not necessarily true that M ≫ K, i.e. there is not always an order of magnitude more antennas than users in massive MIMO.
You are absolutely right! To maximize the sum spectral efficiency it is often preferable to serve relatively many users, with M/K<10. Even if the spectral efficiency per user is not extraordinary, the sum spectral efficiency can be huge.
However, if we want to achieve high spectral efficiency per user, at the cost of lower sum spectral efficiency, we might want to have M/K>10.
Correct: Myth 6…
https://arxiv.org/pdf/1503.06854.pdf
I guess, all mentioned numbers correspond to quasi-static channel conditions (or instant ideal CSI), right? Because channel dynamics brings more and more degradation of SE if many layers are used.
Actually, it could be interesting to discuss the same issues for moving users with Doppler spread 10-20 Hz at least.
In the numerical analysis, we consider Rayleigh fading channels that are static within a coherence block, and independent between blocks. The channel variability is thus captured by the size of the coherence blocks. As you say, more channel dynamics lead to smaller blocks, which in turn give smaller SE.
For any given scenario (carrier frequency, Doppler spread, etc.), you can compute an approximate coherence time and coherence bandwidth, multiply them together and then you have the number of channel uses per coherence block.
Importantly: The Massive MIMO analysis does *not* rely on “ideal CSI” assumptions. Channels are estimated, once per coherence interval, from uplink pilots – and the resulting channel estimation errors (and the pilot overhead) are accounted for in the performance bounds.
Most of the research works consider linear techniques such as ZF, P-ZF, MRC and MMSE to improve the spectral efficiency, where SE is mostly related to SINR and rate. Is there any other techniques to increase SE? Next question is whether DL achievable SE is higher or UL achievable SE?
I would say that there is little need to develop new uplink receive combining or downlink precoding schemes. The schemes that you mention are the ones of main interest. Another way to improve the SE is power control. It can have a substantial impact on the SE:
https://arxiv.org/pdf/1505.03682.pdf
https://arxiv.org/pdf/1509.02633.pdf
https://www.metis2020.com/wp-content/uploads/publications/IEEE_ICC2014_Guo_etal_UplinkPowerControl.pdf
Regarding uplink versus downlink, there is not absolute answer to that question, because there can be substantial transmit power difference between the uplink and downlink. Traditionally, the downlink uses higher power and thereby achieves higher SE. If the total transmit power is the same, then the uplink SE can be larger since the base station has direct access to the channel estimates and can thus decode the signals more accurately.
Hi Emil,
Can you please explain further how BS has direct access to the channel estimation which the MS does have?
The user device transmit a pilot signal in the uplink, which enables channel estimation at the base station.
Thank you Emil Björnson for your sparing your valuable time. I also wonder how to optimize SE and EE in massive MIMO, what is the trade-off between them? Most papers considered the impact of interference when evaluating the SE.
Interference plays an important role, both when evaluating the SE and the EE (energy efficiency). There are several papers that analyzes this tradeoff:
https://arxiv.org/pdf/1112.3810.pdf
https://arxiv.org/pdf/1403.6150.pdf
http://dx.doi.org/10.1109/TVT.2015.2436896
https://arxiv.org/pdf/1505.01181
https://arxiv.org/pdf/1401.4907v4.pdf
The good news is that Massive MIMO can achieve both high SE and EE, since both of these goals are achieved by multiplexing of many UEs, which share the energy costs and achieve a high sum SE. I believe that this is a topic we will return to on the blog.
Sir, can we have the expression for spectral efficiency of massive MIMO?
There are many different expressions for the computing spectral efficiency in Massive MIMO, depending on if it is uplink or downlink, or which processing scheme that is used.
You can find many of these things in Section 4 of my book Massive MIMO Networks, which you can download here: https://massivemimobook.com/wp/
Hi – great website BTW, very helpful.
Sorry for being two months late to this thread, hopefully still open for questions… I’m debating this subject with colleagues, some of whom expect the overall spectral efficiency of a c-band mMIMO sector to be in the 3-6 bps/Hz range, which seems a very long way below what I’m hearing from vendors (and of course the Bristol results). They claim this is due to “real world” adjustments to expected performance, but that seems like a big adjustment. Can such conflicting levels of SE performance be explained? Perhaps currently available mMIMO equipment doesn’t implement digital beamforming, and hence no effective MU capability? What is the expectation of equipment evolution with respect to support for more effective spatial multiplexing – over the next 5 yeats for instance?
Many thanks
3-6 bps/Hz is what you can achieve for single-user transmission under good conditions. Uncoded 64-QAM transmission gives 6 bps/Hz.
Hence, I think your colleagues are having single-user transmission with massive beamforming in mind.
By spatially multiplexing, say, 8 users the overall spectral efficiency will rather be in the range of 24-48 bps/Hz.
Hi Emil,
By uncoding/coding I guess here you indicated to channel coding. How channel coding impacts the spectral efficiency?
When the channel supports a particular spectral efficiency, you need to find a modulation+coding scheme that delivers that spectral efficiency. For example, if you support 5 bit/s/Hz, then you can pick 64-QAM (6 bit/s/Hz) and then apply a channel code with rate 5/6.
sir, what are the objectives of spectral efficiency
The data rate is computed as “spectral efficiency” multiplied with “bandwidth”. Since the bandwidth is often determined by external factors such as licenses, the spectral efficiency is determining how efficiently the technology itself operates.
Dear Prof.
Thank you so much for you this website and your book on massive MIMO networks. I am learning a lot of things from this book, as I am new in this field.
Matlab codes of all figures are given except Figure 7.1 (Example of an SE region (shaded) with different combinations of SEs).
I would like to request you please can you provide the Matlab code of Figure 7.1 also, because as a beginner, I think this will help the students who start to learn massive MIMO.
Thanks in advance
This figure is mainly drawn in Adobe Illustrator as an illustration, so that is why we don’t have any simulation code for it. But if you want to learn how to generate rate regions like this, I recommend my previous book “Optimal Resource Allocation in Coordinated Multi-Cell Systems”. Figure 3.1 generates rate regions and there is simulation code that reproduces these figures, or at least figures of the same kind (the exact region depends on the random seed).
Dear professor
Thanks a lot for creating such a wonderful platform and for the book “Massive MIMO Networks”. This book is very helpful for me as I am new in this field. I have seen most of your books and journals related to massive MIMO. Currently, I am doing my thesis on spectral and energy efficiency in massive mimo. But I also want to show a relative study between Massive MIMO and Massive MIMO-OFDM in my work. So I want to write all the equations (like SE, EE, and circuit power consumption equations) for Massive MIMO-OFDM for “N” subcarriers too. Can you please suggest me some good papers related to this? I will be always grateful to you.
Thanks
Thank you for reading the book!
The block-fading model that we are considering is an abstraction of OFDM that captures its essential properties (e.g., the channels vary over frequency, and all the subcarriers within the coherence bandwidth are placed in the same coherence block) but without the complicated math. Writing all the same things using an exact MIMO-OFDM notation will be much, much more complicated.
The introduction chapters to the thesis “High-end performance with low-end hardware: Analysis of massive MIMO base station transceivers” explains some of the things rather nicely.
One of the relevant papers in the thesis is “Waveforms for the Massive MIMO Downlink:Amplifier Efficiency, Distortion and Performance“.
Thank you so much for this article. I was wondering where I can get the Matlab code for the simulation in this article sir?
Dear Professor Bjornson
I have a question. As we know massive MIMO works based on SDMA and here we have the adjacent cells that serve users on the same frequency. Is not it in conflict with the classic definition of cell?
Can I ask what is the define of a cell in a massive MIMO network?
Regards
A cell is the geographical region where the users will connect to the base station that controls that cell. It is the same definition in Massive MIMO as other types of networks.
Maybe what you are thinking about is that traditional cellular networks divided the radio resources using frequency division. For example, each cell might only use 1/4 of the frequencies, to avoid that neighboring cells use the same frequency and interfere too much. Nowadays, we use beamforming (a key part of SDMA) to limit the inter-cell interference and therefore we can a full reuse of frequencies between all cells.
Dear Professor Bjornson
I have seen most of your books and journals I appreciate you mostly. Now I am doing my thesis on spectral efficiency analysis. In my work, I want to show the effect of code block length on SE. Can you help me? I want some simulation code like the effect of code block length on SE.
What we call spectral efficiency is normally an achievable lower bound on the channel capacity, which means that it is achieved as the block length goes to infinity. Hence, I don’t know how connect SE with the block length as you are suggesting.
Perhaps a better option would be to relate to BER with the code block length. You can simulate such thing using Sionna: https://nvlabs.github.io/sionna/
Hi! I might be rusty in comm theory but from my understanding with 20 MHz channel, 256-QAM and with as many rx and tx antennas I don’t understand where the massive increase in spectral efficiency comes from as from definition spectral efficiency is bit/s/Hz assuming log2 of 256 bits =8 so spectral eff is 8 bits/s/Hz can some one please correct me or explain where the over 100 bits/s/Hz is coming thanks
Hi! If you can send 256-QAM signals to 22 users simulateneously, the spectral efficiency per user is 8 bit/s/Hz and the total spectral efficency is 8*22 = 176 bit/s/Hz.
Massive MIMO enables you to serve the users at the same time and frequency, and protects their signals from interference using beamforming/precoding/combining (many names for roughtly the same thing).
I understand with spatial multiplexing it is possible but with beamforming MIMO how do they get such high spectral efficiency as beamforming is just advanced constructive interference but its not spatial multiplexing or does the increased SNR from beamforming allow for spatial multiplexing thanks again?
With multi-user beamforming/precoding/combining, you can achieve constructive interference at the desired locations and destructive interference at the undesired location. In this way, you can communicate with many users at the same time and frequency, almost as if they were alone. This is the spatial multiplexing.
Hi Sir!!! Very intersting topic. Just a question
Is it really possible to achieve those capacities in real environments?
For average throughput gain, what kind of improvement can we expect comparing it to 2×2 MIMO? I have read somewhere that it is like 3x.
The values were obtained by measurements so they can be achieved in real environments, but it will not be the average performance.
With 2×2 MIMO, you can ideally transmit 2 layers of data without interference. This leads to 2x the capacity compared to 1×1 SISO.