Adaptive beamforming for wireless communications has a long history, with the modern research dating back to the 70s and 80s. There is even a paper from 1919 that describes the development of directive transatlantic communication practices that were developed during the First World War. Many of the beamforming methods that are considered today can be found already in the magazine paper Beamforming: A Versatile Approach to Spatial Filtering from 1988. Plenty of further work was carried out in the 90s and 00s, before the Massive MIMO paradigm.
I think it is fair to say that no fundamentally new beamforming methods have been developed in the Massive MIMO literature, but we have rather taken known methods and generalized them to take imperfect channel state information and other practical aspects into account. And then we have developed rigorous ways to quantify the achievable rates that these beamforming methods achieve and studied the asymptotic behaviors when having many antennas. Closed-form expressions are available in some special cases, while Monte Carlo simulations can be used to compute these expressions in other cases.
As beamforming has evolved from an analog phased-array concept, where angular beams are studied, to a digital concept where the beamforming is represented in multi-dimensional vector spaces, it easy to forget the basic properties of array processing. That is why we dedicated Section 7.4 in Massive MIMO Networks to describe how the physical beam width and spatial resolution depend on the array geometry.
In particular, I’ve observed a lot of confusion about the dimensionality of MIMO arrays, which are probably rooted in the confusion around the difference between an antenna (which is something connected to an RF chain) and a radiating element. I explained this in detail in a previous blog post and then exemplified it based on a recent press release. I have also recorded the following video to visually explain these basic properties:
A recent white paper from Ericsson is also providing a good description of these concepts, particularly focused on how an array with a given geometry can be implemented with different numbers of RF chains (i.e., different numbers of antennas) depending on the deployment scenario. While having as many antennas as radiating element is preferable from a performance perspective, but the Ericsson researchers are arguing that one can get away with fewer antennas in the vertical direction in deployments where it is anyway very hard to resolve users in the elevation dimension.

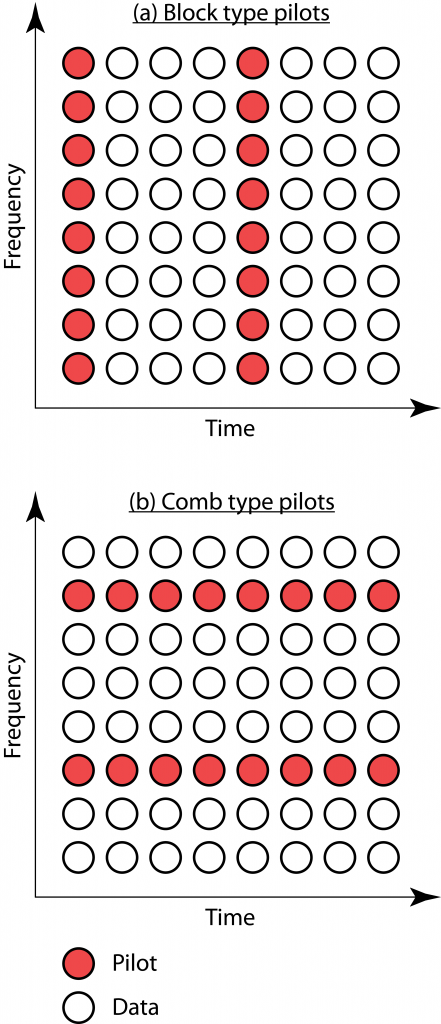
 In this case, the BS tries out a set of different precoding vectors from a codebook (e.g., a grid of beams, as shown to the right) by sending one downlink pilot signal through each one of them. The user measures
In this case, the BS tries out a set of different precoding vectors from a codebook (e.g., a grid of beams, as shown to the right) by sending one downlink pilot signal through each one of them. The user measures  In this case, the user transmits a pilot signal in the uplink, which enables the BS to directly estimate the entire channel vector
In this case, the user transmits a pilot signal in the uplink, which enables the BS to directly estimate the entire channel vector