Since its inception, Massive MIMO has been strongly connected with asymptotic analysis. Marzetta’s seminal paper featured an unlimited number of base station antennas. Many of the succeeding papers considered a finite number of antennas, , and then analyzed the performance in the limit where . Massive MIMO is so tightly connected with asymptotic analysis that reviewers question whether a paper is actually about Massive MIMO if it does not contain an asymptotic part – this has happened to me repeatedly.

Have you reflected over what the purpose of asymptotic analysis is? The goal is not that we should design and deploy wireless networks with a nearly infinite number of antennas. Firstly, it is physically impossible to do that in a finite-sized world, irrespective of whether you let the array aperture grow or pack the antennas more densely. Secondly, the conventional channel models break down, since you will eventually receive more power than you transmitted. Thirdly, the technology will neither be cost nor energy efficient, since the cost/energy grows linearly with , while the delivered system performance either approaches a finite limit or grows logarithmically with .

It is important not to overemphasize the implications of asymptotic results. Consider the popular power-scaling law which says that one can use the array gain of Massive MIMO to reduce the transmit power as and still approach a non-zero asymptotic rate limit. This type of scaling law has been derived for many different scenarios in different papers. The practical implication is that you can reduce the transmit power as you add more antennas, but the asymptotic scaling law does not prescribe how much you should reduce the power when going from, say, 40 to 400 antennas. It all depends on which rates you want to deliver to your users.

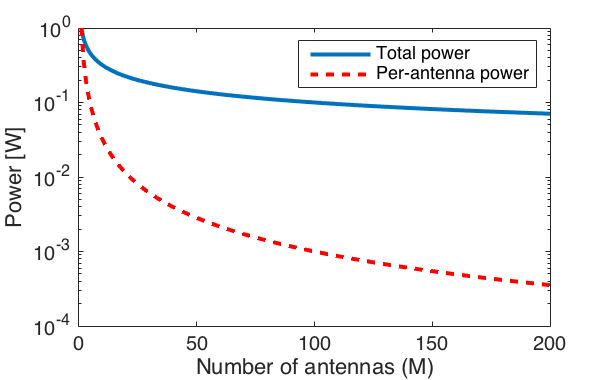
The figure below shows the transmit power in a scenario where we start with 1 W for a single-antenna transmitter and then follow the asymptotic power-scaling law as the number of antennas increases. With  antennas, the transmit power per antenna is just 1 mW, which is unnecessarily low given the fact that the circuits in the corresponding transceiver chain will consume much more power. By using higher transmit power than 1 mW per antenna, we can deliver higher rates to the users, while barely effecting the total power of the base station.

Similarly, there is a hardware-scaling law which says that one can increase the error vector magnitude (EVM) proportionally to and approach a non-zero asymptotic rate limit. The practical implication is that Massive MIMO systems can use simpler hardware components (that cause more distortion) than conventional systems, since there is a lower sensitivity to distortion. This is the foundation on which the recent works on low-bit ADC resolutions builds (see this paper and references therein).

Even the importance of the coherent interference, caused by pilot contamination, is easily overemphasized if one only considers the asymptotic behavior.  For example, the finite rate limit that appears when communicating over i.i.d. Rayleigh fading channels with maximum ratio or zero-forcing processing is only approached in practice if one has around one million antennas.

In my opinion, the purpose of asymptotic analysis is not to understand the asymptotic behaviors themselves, but what the asymptotics can tell us about the performance at practical number of antennas. Here are some usages that I think are particularly sound:

• Determine what is the asymptotically optimal transmission scheme and then evaluate how it performs in a practical system.
• Derive large-scale approximations of the rates that are reasonable tight also at practical number of antennas. One can use these approximations to determine which factors that have a dominant impact on the rate or to get a tractable way to optimize system performance (e.g., by transmit power allocation).
• Determine how far from the asymptotically achievable performance a practical system is.
• Determine if we can deliver any given user rates by simply deploying enough antennas, or if the system is fundamentally interference limited.
• Simplify the signal processing by utilizing properties such as channel hardening and favorable propagation. These phenomena can be observed already at 100 antennas, although you will never get a fully deterministic channel or zero inter-user interference in practice.

Some form of Massive MIMO will appear in 5G, but to get a well-designed system we need to focus more on demonstrating and optimizing the performance in practical scenarios (e.g., the key 5G use cases) and less on pure asymptotic analysis.