Massive MIMO is all about using large arrays to transmit narrow beams, thereby increasing the received signal power and enabling spatial multiplexing of signals in different directions. Importantly, the words “large” and “massive” have relative meanings in this context: they refer to having many transceiver chains, which leads to many more spatial degrees of freedom in the beamforming design than in previous cellular technologies. However, the physical sizes of the 5G Massive MIMO arrays that are being deployed are similar to previous base station equipment. The reason is that the number of radiating elements is roughly the same and this is what determines the physical size.
What if we would deploy physically large arrays?
Since base station arrays are deployed at elevated places, many tens of meters from the users, 5G antenna arrays will look small from the viewpoint of the user. This situation might change in the future, when moving beyond 5G. Suppose we would cover the entire facade of a building with antennas, as illustrated in Figure 1, then the array would be physically large, not only feature a large number of transceiver chains.
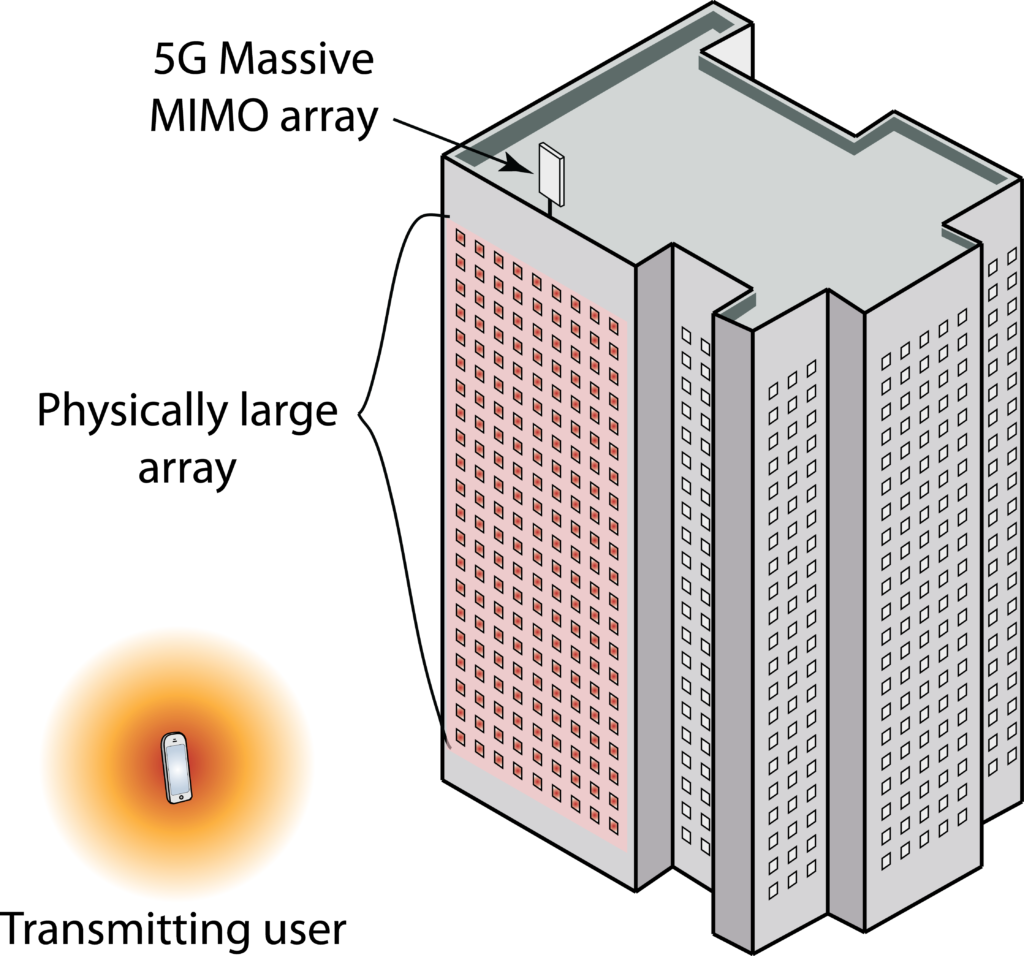
There are unusual wireless propagation phenomena that occur in such deployments and these have caught my attention in recent years. A lot of research papers on Massive MIMO consider the asymptotic regime where the number of antennas (transceiver chains) goes to infinity, but the channel models that are being used break down asymptotically. For example, the received signal power goes to infinity although the transmitted power is finite, which is physically impossible.
This inconsistency was a reason for why I didn’t jump onto the Massive MIMO train when it took off in 2010, but waited until I realized that Marzetta’s mind-blowing asymptotic results are also applicable in many practical situations. For example, if the users are at least ten meters away from the base station, we can make use of thousands of antennas before any inconsistencies arise. The asymptotic issues have been stuck in my mind ever since but now I have finally found the time and tools needed to characterize the true asymptotic behaviors.
Three important near-field characteristics
Three phenomena must be properly modeled when the user is close to a physically large array, which we call the array’s near-field. These phenomena are:
- The propagation distance varies between the different antennas in the array.
- The antennas are perceived to have different effective areas since they are observed from different angles.
- The signal losses due to polarisation mismatch vary due to the different angles.
Wireless propagation channels have, of course, always been determined by the propagation distances, effective antenna areas, and polarisation losses. However, one can normally make the approximation that they are equal for all antennas in the array. In our new paper “Power Scaling Laws and Near-Field Behaviors of Massive MIMO and Intelligent Reflecting Surfaces“, we show that all three conditions must be properly modeled to carry out an accurate asymptotic study. The new formulas that we present are confirming the intuition that the part of the array that is closest to the user is receiving more power than the parts that are further away. As the array grows infinitely large, the outer parts receive almost nothing and the results comply with fundamental physics, such as the law of conservation of energy.
You might have heard about the Fraunhofer distance, which is the wavelength-dependent limit between the near-field and far-field of a single antenna. This distance is not relevant in our context since we are not considering the radiative behaviors that occur close to an antenna, but the geometric properties of a large array. We are instead studying the array’s near-field, when the user perceives an electrically large array. The result is wavelength-independent and occurs approximately when the propagation distance is shorter than the widest dimension of the array. This is when one must take the three properties above into account to get accurate results. Note that it is not the absolute size of the array that matters but how large it is compared to the field-of-view of the user.
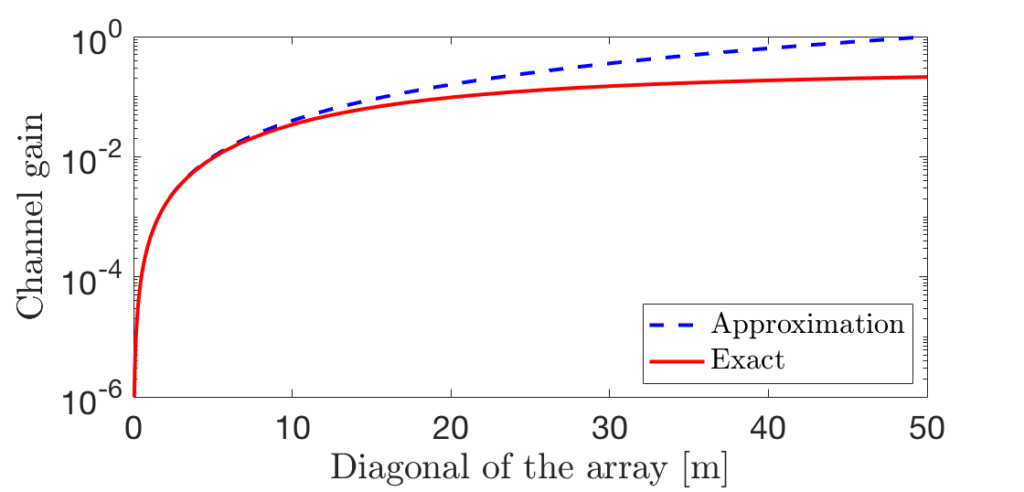
Figure 2 illustrates this property by showing the channel gain (i.e., the fraction of the transmitted power that is received) in a setup with an isotropic transmit antenna that is 10 m from the center of a square array. The diagonal of the array is shown on the horizontal axis. The solid red curve is computed using our new accurate formula, while the blue dashed curve is based on the conventional far-field approximation. The curves are overlapping until the diagonal is 10 m (same as the propagation distance). The difference increases rapidly when the array becomes larger (notice the logarithmic scale on the vertical axis). When the diagonal is 50 m, the approximation errors are extreme: the channel gain surpasses 1, which means that more power is received than was transmitted.
There are practical applications
There are two ongoing lines of research where the new near-field results and insights are useful, both to consolidate the theoretical understanding and from a practical perspective.
One example is the physically large and dense Massive MIMO arrays which are being called large intelligent surfaces and holographic MIMO. These names are utilized to distinguish the analysis from the physically small Massive MIMO products that are now being deployed in 5G. Another example is the “passive” metasurface-based arrays that are being called reconfigurable intelligent surfaces and intelligent reflecting surfaces. These are arrays of scattering elements that can be configured to scatter an incoming signal from a transmitter towards a receiver.
We are taking a look at both of these areas in the aforementioned paper. In fact, the reason why we initiated the research last year is that we wanted to understand how to compare the asymptotic behaviors of the two technologies, which exhibit different power scaling laws in the far-field but converge to similar limits in the array’s near-field.
If you would like to learn more, I recommend you to read the paper and play around with the simulation code that you can find on GitHub.

Hello, Professor.Bjornson
Specially thank you for your good posts.
Could you please explain more about electrically large arrays?
Is there anything particular that you think we should write about?
Here is by the way a recent preprint of a magazine paper: https://arxiv.org/pdf/2012.01315.pdf
Thank you very much for introducing this paper. I understood the concept . Thank you