For the last five years, most of the research into wireless communications has been motivated by its potential role in 6G. As standardization efforts begin in 3GPP this year, we will discover which of the so-called “6G enablers” has attracted the industry’s attention. Probably, only a few new technology components will be introduced in the first 6G networks in 2029, and a few more will be gradually introduced over the next decade. In this post, I will provide some brief predictions on what to expect.

6G Frequency Band

In December 2023, the World Radiocommunication Conference identified three potential 6G frequency bands, which will be analyzed until the next conference in 2027 (see the image below). Hence, the first 6G networks will operate in one of these bands if nothing unforeseen happens. The most interesting new band is around 7.8 GHz, where 650-1275 MHz of spectrum might become available, depending on the country.

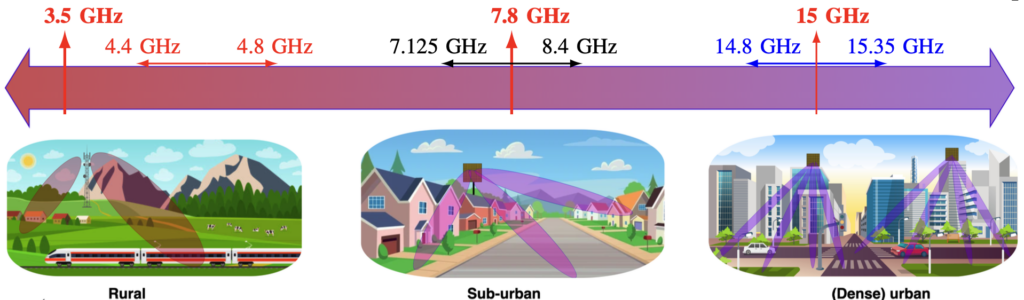
This band belongs to the upper mid-band, the previously overlooked range between the sub-7 GHz and the mmWave bands considered in 5G. It has recently been called the golden band since it offers more spectrum than current 5G networks in the 3.5 GHz band and much better propagation conditions than at mmWave frequencies. But honestly, the new spectrum availability is quite underwhelming: It is around twice the amount that 5G networks will already be using in 2029. Hence, we cannot expect any large capacity boost just from introducing these new bands.

Gigantic MIMO arrays

However, the new frequency bands will enable us to deploy many more antenna elements in the same form factor as current antenna arrays. Since the arrays are two-dimensional, the number grows quadratically with the carrier frequency. Hence, we can expect five times as many antennas in the 7.8 GHz band as at 3.5 GHz, which enables spatial multiplexing of five times more data. When combined with twice the amount of spectrum, we can reach an order of magnitude (10×) higher capacity in the first 6G networks than in 5G.

Since the 5G antenna technology is called “Massive MIMO” and 6G will utilize much larger antenna numbers, we need to find a new adjective. I think “Gigantic MIMO“, abbreviated as gMIMO, is a suitable term. The image below illustrates a 0.5 × 0.5 m array with 25 × 25 antenna elements in the 7.8 GHz band. Since practical base stations often have antenna numbers being a power of two, it is likely we will see at least 512 antenna elements in 6G.

During the last few months, my postdocs and I have looked into what the gMIMO technology could realistically achieve in 6G. We have written a magazine-style paper to discuss the upper mid-band in detail, describe how to reach the envisioned 6G performance targets, and explain what deployment practices are needed to utilize the near-field beamfocusing phenomenon for precise communication, localization, and sensing. We also identify five open research challenges, which we recommend you look into if you want to impact the actual 6G standardization and development.

You can download the paper here: Emil Björnson, Ferdi Kara, Nikolaos Kolomvakis, Alva Kosasih, Parisa Ramezani, and Murat Babek Salman, “Enabling 6G Performance in the Upper Mid-Band Through Gigantic MIMO,” arXiv:2407.05630.

I started analyzing reconfigurable intelligent surfaces (RISs) in 2019, just when the hype began in the communication community. I was mostly interested in understanding the fundamentals of this technology because some claims that I found in papers were too good to be true. In 2020, we summarized our thoughts in the paper “Reconfigurable Intelligent Surfaces: Three Myths and Two Critical Questions,” which corrected three misconceptions that flourished then.

More importantly, we identified two open research problems that we found particularly important to solve if the RIS technology should become practically and commercially viable.

The first question was: What is a Convincing Use Case for RIS? The literature was already full of potential use cases; take any communication scenario and add an RIS, and you will improve the system performance by a little. However, the proposed use cases were either too niche-oriented to motivate technology development or aimed at “solving” problems that existing technology (e.g., relays or small cells) could already manage to some extent. A groundbreaking use case of clear commercial value was missing, and I think we have yet to find it.

The second question was: How can we estimate channels and control a RIS in real time? I was skeptical that it would be possible to solve this problem until I saw a demo video from the University of Surrey in late 2020 and participated in a measurement campaign at the Huazhong University of Science and Technology. I then decided to look for a solution together with my research group at KTH.

Real-time reconfigurability is challenging because a typical RIS has hundreds of elements; thus, there are hundreds of channel parameters to estimate every time the channel changes. A plausible solution is to narrow the scope to use cases where the channels can be parametrized efficiently. If the propagation geometry is such that the channel is determined by the same few parameters, regardless of how many RIS elements there are, we can focus on estimating those parameters instead. We realized that array signal processing contains the necessary tools for developing such geometry-based models and algorithms.

We now have a solid solution framework. In the following video, I explain our approach, from the first principles to the solution. The slides were originally prepared for a keynote speech at IEEE CAMSAP 2023 and then fine-tuned for my recent keynote at IEEE SITB 2024.

The technical details are found in the paper “Parametric Channel Estimation with Short Pilots in RIS-Assisted Near- and Far-Field Communications,” which will appear in the IEEE Transactions on Wireless Communications in 2024.

The research community often praises reconfigurable intelligent surfaces (RISs) as a transformative technology. By controlling parts of wireless propagation channels, we can improve the bit rates by increasing the received signal strength, mitigating interference, enhancing channel ranks, etc. The potential benefits RISs can bring to wireless networks are now well documented, and several of them have also been demonstrated experimentally. However, the RIS technology also introduces several practical complications that one must be mindful of. In this blog post, I will give two examples of the dark side of the RIS technology.

Pilot contamination between operators

Suppose a telecom operator deploys an RIS to enhance the performance experienced by its customers. The academic literature is full of algorithms that can be used to that end. Each time the operator changes the RIS configuration, it will affect not only the wireless channels within its licensed frequency band but also the channels in many neighboring bands. The phase-shifting in each RIS element acts as an approximately linear-phase filtering operation, which shifts the phases of reflected signals (proportionally to their carrier frequencies) both in the intended and adjacent bands. Since there is no non-linear distortion, the operator’s wireless signals are maintained in their designated band. Nevertheless, the operator messes with the channel characteristics in neighboring bands every time it reconfigures its RIS. In the best-case scenario, the systems operating in neighboring bands only experience additional fading variations. In the worst-case scenario, they will suffer from substantial performance degradation.

An instance of the latter scenario appears when two telecom operators deploy RISs in the same coverage area. We studied this scenario in a recent paper. 5G networks typically use time-division duplex (TDD) bands, and the operators are time-synchronized, so they switch between uplink and downlink simultaneously. This implies that the considered operators will send pilot sequences in parallel, which is usually fine because they are transmitted in different bands. However, if each operator uses its pilot sequences for RIS reconfiguration that helps its own users, it will also modify the other operator’s channels in undesired ways after the estimation has occurred. This leads to a new kind of pilot contamination effect, which differs from that in Massive MIMO but leads to the same bottlenecks: reduced estimation quality and a performance limit at high signal-to-noise ratios (SNRs). Consequently, if a large-scale deployment of RIS occurs in cellular networks, we will see not only the intended performance improvements but also occasional unexpected degradations. More research is needed to quantify this effect and what can be done to mitigate it.

Malicious RIS

While the pilot contamination caused between telecom operators is an unintentional disturbance, RIS could also be used for intentional “silent” jamming. In a recent paper, we analyze the situation where a hacker takes control of an operator’s RIS and turns it into a malicious RIS. Instead of maximizing the received signal strength at a specific user device, the RIS can be configured to minimize the signal strength. Since this is achieved by causing destructive interference over the air, the user device will perceive this as having poor coverage. Conventional jamming builds on sending a strongly interfering signal to prevent data decoding, and this can be easily detected. By contrast, the silent jamming caused by a malicious RIS is hard to detect since it destroys the channel without introducing new signals. In our paper, we demonstrate how a malicious RIS can avoid detection by only destroying the channel for one user device while other devices are unaffected. We also show that malicious reflection is possible even if the RIS has imperfect channel knowledge.

In summary, there is a dark side to the RIS technology. It can both manifest itself through unintentional tampering with the channels in neighboring frequency bands and through the risk that an RIS is hacked and turned into a malicious RIS that degrades rather than improves communication performance. Careful regulation, standardization, hardware design, and security will be required to overcome these challenges.