The cellular network that my smartphone connects to normally delivers 10-40 Mbit/s. That is sufficient for video-streaming and other applications that I might use. Unfortunately, I sometimes have poor coverage and then I can barely download emails or make a phone call. That is why I think that providing ubiquitous data coverage is the most important goal for 5G cellular networks. It might also be the most challenging 5G goal, because the area coverage has been an open problem since the first generation of cellular technology.
It is the physics that make it difficult to provide good coverage. The transmitted signals spread out and only a tiny fraction of the transmitted power reaches the receive antenna (e.g., one part of a billion parts). In cellular networks, the received signal power reduces roughly as the propagation distance to the power of four. This results in the following data rate coverage behavior:
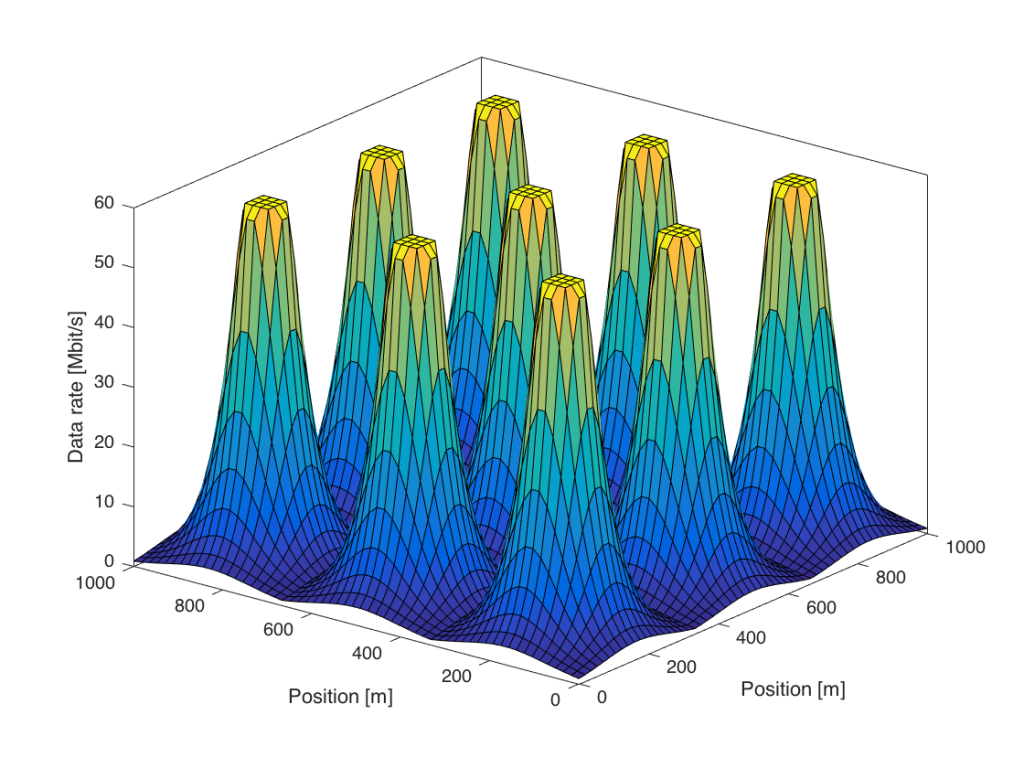
This figure considers an area covered by nine base stations, which are located at the middle of the nine peaks. Users that are close to one of the base stations receive the maximum downlink data rate, which in this case is 60 Mbit/s (e.g., spectral efficiency 6 bit/s/Hz over a 10 MHz channel). As a user moves away from a base station, the data rate drops rapidly. At the cell edge, where the user is equally distant from multiple base stations, the rate is nearly zero in this simulation. This is because the received signal power is low as compared to the receiver noise.
What can be done to improve the coverage?
One possibility is to increase the transmit power. This is mathematically equivalent to densifying the network, so that the area covered by each base station is smaller. The figure below shows what happens if we use 100 times more transmit power:
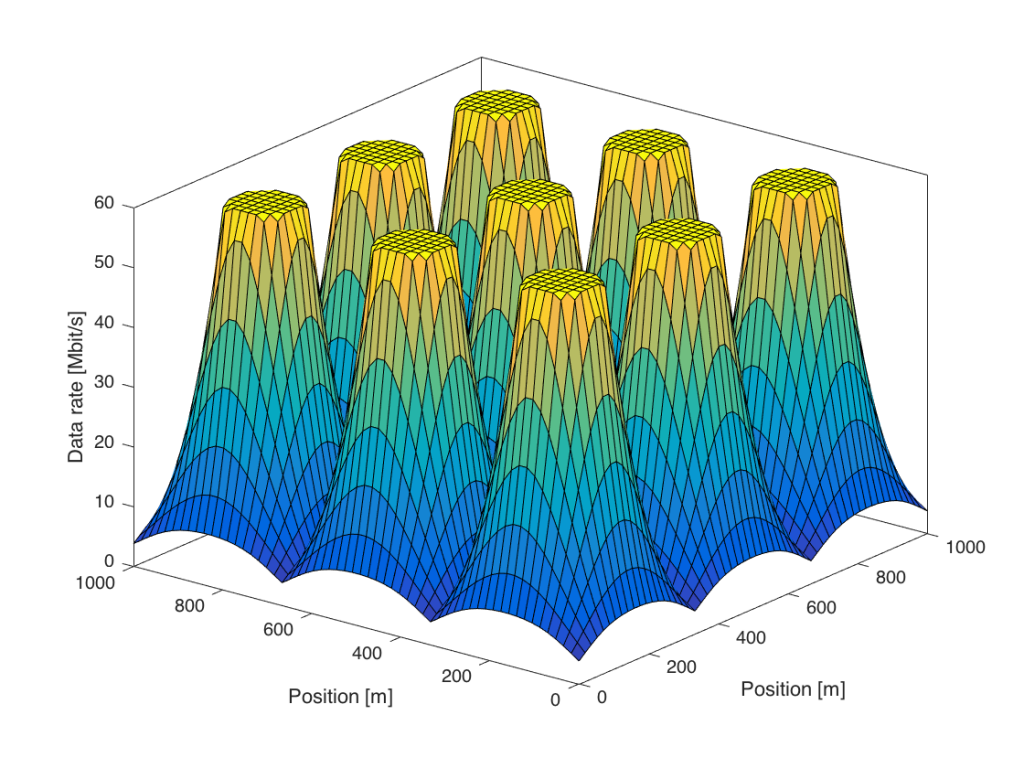
There are some visible differences as compared to Figure 1. First, the region around the base station that gives 60 Mbit/s is larger. Second, the data rates at the cell edge are slightly improved, but there are still large variations within the area. However, it is no longer the noise that limits the cell-edge rates—it is the interference from other base stations.
The inter-cell interference remains even if we would further increase the transmit power. The reason is that the desired signal power as well as the interfering signal power grow in the same manner at the cell edge. Similar things happen if we densify the network by adding more base stations, as nicely explained in a recent paper by Andrews et al.
Ideally, we would like to increase only the power of the desired signals, while keeping the interference power fixed. This is what transmit precoding from a multi-antenna array can achieve; the transmitted signals from the multiple antennas at the base station add constructively only at the spatial location of the desired user. More precisely, the signal power is proportional to M (the number of antennas), while the interference power caused to other users is independent of M. The following figure shows the data rates when we go from 1 to 100 antennas:
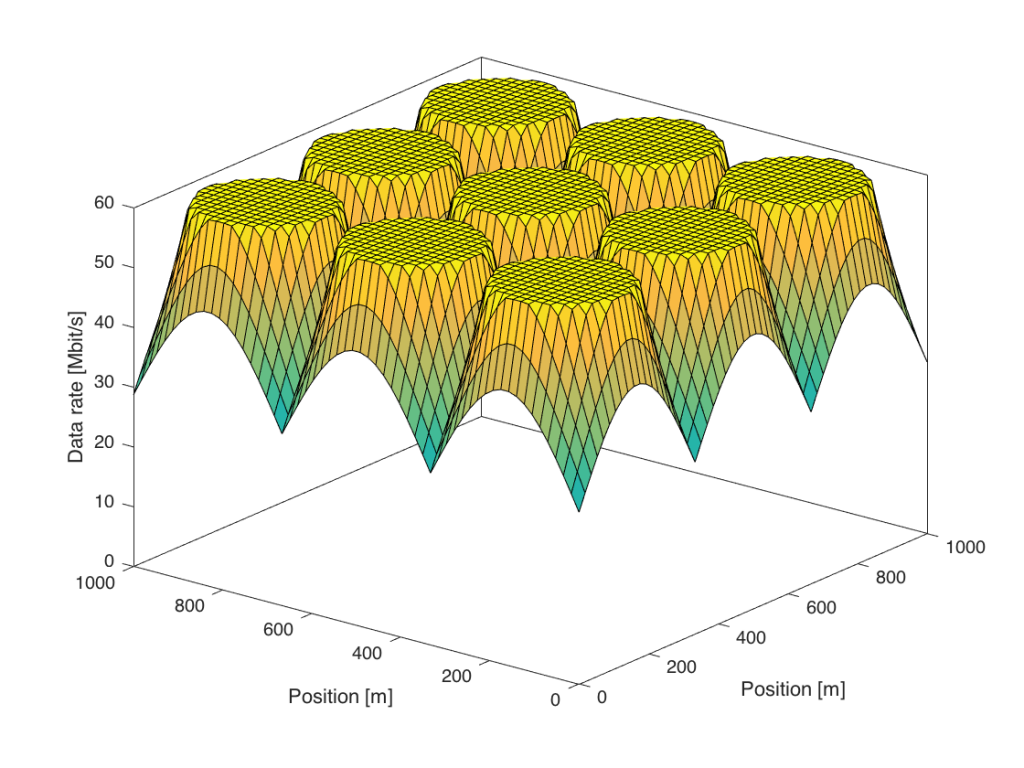
Figure 3 shows that the data rates are increased for all users, but particularly for those at the cell edge. In this simulation, everyone is now guaranteed a minimum data rate of 30 Mbit/s, while 60 Mbit/s is delivered in a large fraction of the coverage area.
In practice, the propagation losses are not only distant-dependent, but also affected by other large-scale effects, such as shadowing. The properties described above remain nevertheless. Coherent precoding from a base station with many antennas can greatly improve the data rates for the cell edge users, since only the desired signal power (and not the interference power) is increased. Higher transmit power or smaller cells will only lead to an interference-limited regime where the cell-edge performance remains to be poor. A practical challenge with coherent precoding is that the base station needs to learn the user channels, but reciprocity-based Massive MIMO provides a scalable solution to that. That is why Massive MIMO is the key technology for delivering ubiquitous connectivity in 5G.

The post is interesting, I appreciate it. Now how can we estimate the cost of using massive mimo in terms of space, in other words will implementing massive MIMO not be challenging in small platform base stations?
It all depends on how many antennas you want to deploy, at what frequency, and what the maximum form factor is. But Massive MIMO is certainly feasible at cellular frequencies, such as 1-5 GHz. You can read more about this in “Myth 1” in the paper:
Emil Björnson, Erik G. Larsson, Thomas L. Marzetta, “Massive MIMO: Ten Myths and One Critical Question,” IEEE Communications Magazine, vol. 54, no. 2, pp. 114-123, February 2016.
Hello, Professor Bjornson.
I have a question related to one of your recent paper where you turn off some APs in a cell-free system to have an energy efficient system.
A question that arise to my mind is that Is and how such a scenario implemented in practice?
Is there an intelligent algorithm that turn off some of the APs in each coherence block?
The paper is considering the ergodic spectral efficiency as the performance metric, which means that the same APs and users are active for many coherence blocks. We are providing an algorithm for determining which APs to activate. This can be done in practice and probably implemented on top of 5G.
5G systems have a feature called Cell discontinuous transmission (DTX) where the cell is put into sleep mode part of the time to save energy. When its service is not needed it only wakes up to transmit control signals, so that new users can connect to the cell.
Hello, professor Bjornson.
I have two questions related to Section 1 of your book.
1) As you say in the section one of the book, an infinite decoding delay is required to achieve the channel capacity in practice.
Can you explain why it should be satisfied this condition to achieve the capacity in practice?
2) Other question is that as you mentioned in the book, to have ergodic capacity, we should have the stationary ergodic fading channel.
What problem is caused if the channel is not ergodic?
Especially, can we define the capacity for a random channel that is not ergodic?
1) This is explained in the sentence before that statement: “If the scalar input has an SE smaller or equal to the capacity, the information sequence can be encoded such that the receiver can decode it with arbitrarily low error probability as N → ∞.” In practice, it is enough to transmit a few thousand bits to operate close to the capacity (i.e., obtain a small but non-zero error probability). Section 1 in Fundamentals of Massive MIMO provides a plot about this.
2) If the channel is non-ergodic, then you cannot predict which ensemble of channel realizations that you will get during the transmission so you cannot encode that data under the assumption that you know the channel statistics. I don’t know how to define the capacity in this case.
Hello Professor Bjornson.
Thank you for your answer.
1) Can you explain why it requires that N tends to infinity to have the decoding with arbitrary low error probability?
2) Also can you explain how the ergodicity of the channel define? And the assumption that the channel is stationary and ergodic to some extent is practical? Especially when the channel is fast fading.
1) This is the classical noisy-channel coding theorem, which is the foundation of everything that has to do with channel capacities: https://en.wikipedia.org/wiki/Noisy-channel_coding_theorem
2) Ergodicity and stationarity are concepts in statistics, see for example https://en.wikipedia.org/wiki/Ergodic_process
The random description of channels is just a model, but a good one.