I attended GLOBECOM in Singapore earlier this week. Since more and more preprints are posted online before conferences, one of the unique features of conferences is to meet other researchers and attend the invited talks and interactive panel discussions. This year I attended the panel “Massive MIMO – Challenges on the Path to Deployment”, which was organized by Ian Wong (National Instruments). The panelists were Amitava Ghosh (Nokia), Erik G. Larsson (Linköping University), Ali Yazdan (Facebook), Raghu Rao (Xilinx), and Shugong Xu (Shanghai University).
No common definition
The first discussion item was the definition of Massive MIMO. While everyone agreed that the main characteristic is that the number of controllable antenna elements is much larger than the number of spatially multiplexed users, the panelists put forward different additional requirements. The industry prefers to call everything with at least 32 antennas for Massive MIMO, irrespective of whether the beamforming is constructed from codebook-based feedback, grid-of-beams, or by exploiting uplink pilots and TDD reciprocity. This demonstrates that Massive MIMO is becoming a marketing term, rather than a well-defined technology. In contrast, academic researchers often have more restrictive definitions; Larsson suggested to specifically include the TDD reciprocity approach in the definition. This is because it is the robust and overhead-efficient way to acquire channel state information (CSI), particularly for non-line-of-sight users; see Myth 3 in our magazine paper. This narrow definition clearly rules out FDD operation, as pointed out by a member of the audience. Personally, I think that any multi-user MIMO implementation that provides performance similar to the TDD-reciprocity-based approach deserves the Massive MIMO branding, but we should not let marketing people use the name for any implementation just because it has many antennas.

Important use cases
The primary use cases for Massive MIMO in sub-6 GHz bands are to improve coverage and spectral efficiency, according to the panel. Great improvements in spectral efficiency have been demonstrated by prototyping, but the panelist agreed that these should be seen as upper bounds. We should not expect to see more than 4x improvements over LTE in the first deployments, according to Ghosh. Larger gains are expected in later releases, but there will continue to be a substantial gap between the average spectral efficiency observed in real cellular networks and the peak spectral efficiency demonstrated by prototypes. Since Massive MIMO achieves its main spectral efficiency gains by multiplexing of users, we might not need a full-blown Massive MIMO implementation today, when there are only one or two simultaneously active users in most cells. However, the networks need to evolve over time as the number of active users per cell grows.
In mmWave bands, the panel agreed that Massive MIMO is mainly for extending coverage. The first large-scale deployments of Massive MIMO will likely aim at delivering fixed wireless broadband access and this must be done in the mmWave bands; there is too little bandwidth in sub-6 GHz bands to deliver data rates that can compete with wired DSL technology.
Initial cost considerations
The deployment cost is a key factor that will limit the first generations of Massive MIMO networks. Despite all the theoretic research that has demonstrated that each antenna branch can be built using low-resolution hardware, when there are many antennas, one should not forget the higher out-of-band radiation that it can lead to. We need to comply with the spectral emission masks – spectrum is incredibly expensive so a licensee cannot accept interference from adjacent bands. For this reason, several panelists from the industry expressed the view that we need to use similar hardware components in Massive MIMO as in contemporary base stations and, therefore, the hardware cost grows linearly with the number of antennas. On the other hand, Larsson pointed out that the futuristic devices that you could see in James Bond movies 10 years ago can now be bought for $100 in any electronic store; hence, when the technology evolves and the economy of scale kicks in, the cost per antenna should not be more than in a smartphone.
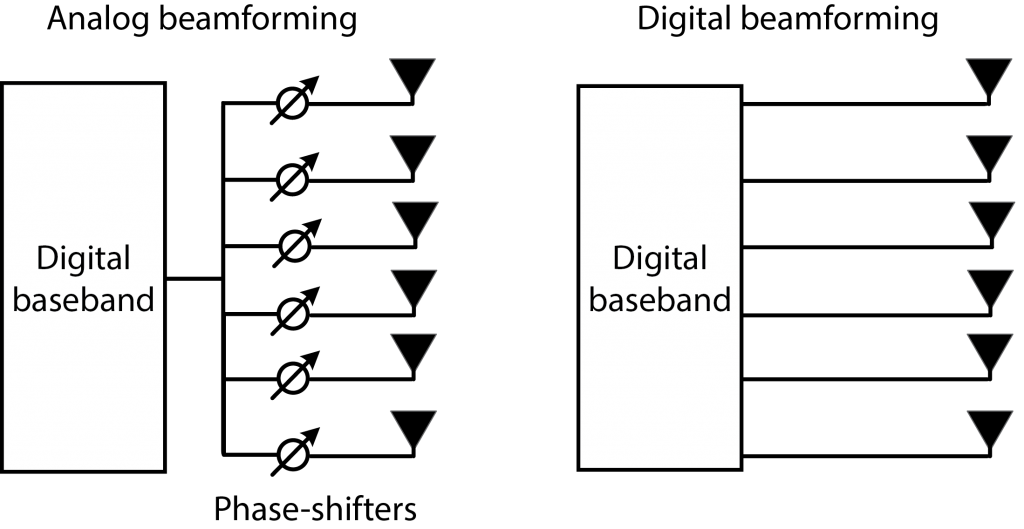
A related debate is the one between analog and digital beamforming. Several panelists said that analog and hybrid approaches will be used to cut cost in the first deployments. To rely on analog technology is somewhat weird in an age when everything is becoming digital, but Yazdan pointed out that it is only a temporary solution. The long-term vision is to do fully digital beamforming, even in mmWave bands.
Another implementation challenge that was discussed is the acquisition of CSI for mobile users. This is often brought up as a showstopper since hybrid beamforming methods have such difficulties – it is like looking at a running person in a binocular and trying to follow the movement. This is a challenging issue for any radio technology, but if you rely on uplink pilots for CSI acquisition, it will not be harder than in a system of today. This has also been demonstrated by measurements.
Open problems
The panel was asked to describe the most important open problems in the Massive MIMO area, from a deployment perspective. One obvious issue, which we called the “grand question” in a previous paper, is to provide better support for Massive MIMO in FDD.
The control plane and MAC layer deserve more attention, according to Larsson. Basic functionalities such as ACK/NACK feedback is often ignored by academia, but incredibly important in practice.
The design of “cell-free” densely distributed Massive MIMO systems also deserve further attention. Connecting all existing antennas together to perform joint transmission seems to be the ultimate approach to wireless networks. Although there is no practical implementation yet, Yazdan stressed that deploying such networks might actually be more practical than it seems, given the growing interest in C-RAN technology.
10 years from now
I asked the panel what will be the status of Massive MIMO in 10 years from now. Rao predicted that we will have Massive MIMO everywhere, just as all access point supports small-scale MIMO today. Yazdan believed that the different radio technology (e.g., WiFi, LTE, NR) will converge into one interconnected system, which also allows operators to share hardware. Larsson thinks that over the next decade many more people will have understood the fundamental benefits of utilizing TDD and channel reciprocity, which will have a profound impact on the regulations and spectrum allocation.

 After the
After the