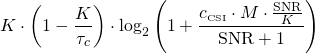No, these are two different but somewhat related concepts, as I will explain in detail below.
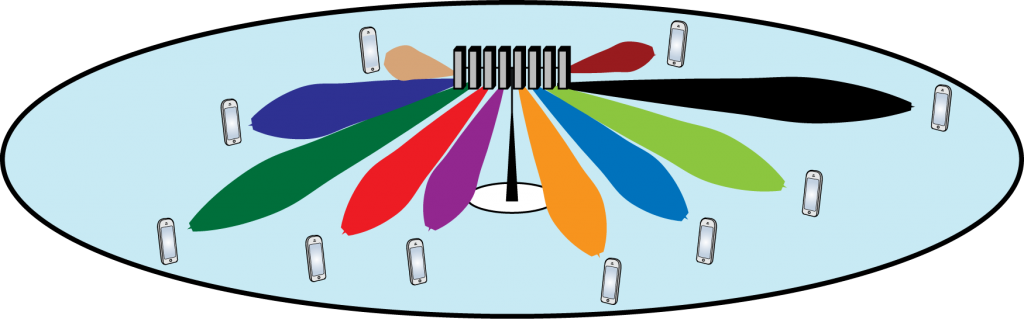
Contemporary multiantenna base stations for cellular communications are equipped with 2-8 antennas, which are deployed along a horizontal line. One example is a uniform linear array (ULA), as illustrated in Figure 1 below, where the antenna spacing is uniform. All the antennas in the ULA have the same physical down-tilt, with respect to the ground, and a fixed radiation pattern and directivity.
By sending the same signal from all antennas, but with different phase-shifts, we can steer beams in different angular directions and thereby make the directivity of the radiated signal different from the directivity of the individual antennas. Since the antennas are deployed on a one-dimensional horizontal line in this example, the ULA can only steer beams in the two-dimensional (2D) azimuth plane as illustrated in Figure 1. The elevation angle is the same for all beams, which is why this is called 2D beamforming. The beamwidth in the azimuth domain shrinks the more antennas are deployed. If the array is used for multiuser MIMO, then multiple beams with different azimuth angles are created simultaneously, as illustrated by the colored beams in Figure 1.

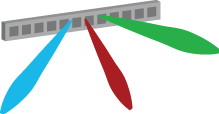
If we would rotate the ULA so that the antennas are instead deployed at different heights above the ground, then the array can instead steer beams in different elevation angles. This is illustrated in Figure 2. Note that this is still a form of 2D beamforming since every beam will have the same directivity with respect to the azimuth plane. This antenna array can be used to steer beams towards users at different floors of a building. It is also useful to serve flying objects, such as UAVs, jointly with ground users. The beamwidth in the elevation domain shrinks the more antennas are deployed.

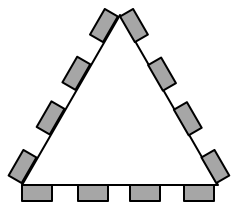
If we instead deploy multiple ULAs on top of each other, it is possible to control both the azimuth and elevation angle of a beam. This is called 3D beamforming (or full-dimensional MIMO) and is illustrated in Figure 3 using a planar array with a “massive” number of antennas. This gives the flexibility to not only steer beams towards different buildings but also towards different floors of these buildings, to provide a beamforming gain wherever the user is in the coverage area. It is not necessary to have many antennas to perform 3D beamforming – it is basically enough to have three antennas deployed in a triangle. However, as more antennas are added, the beams become narrower and easier to jointly steer in specific azimuth-elevation directions. This increases the array gain and reduces the interference between beams directed to different users, as illustrated by the colors in Figure 3.
The detailed answer to the question “3D Beamforming, is that Massive MIMO?” is as follows. Massive MIMO and 3D beamforming are two different concepts. 3D beamforming can be performed with few antennas and Massive MIMO can be deployed to only perform 2D beamforming. However, Massive MIMO and 3D beamforming is a great combination in many applications; for example, to spatially multiplex many users in a city with high-rise buildings. One should also bear in mind that, in general, only a fraction of the users are located in line-of-sight so the formation of angular beams (as shown above) might be of limited importance. The ability to control the array’s radiation pattern in 3D is nonetheless helpful to control the multipath environment such that the many signal components add constructively at the location of the intended receiver.


 The picture above shows a real LTE site that I found in Nanjing, China, a couple of years ago. Looking at it from above, the site is structured as illustrated to the right. The site consists of three sectors, each containing a base station with four vertical panels. If you would look inside one of the panels, you will (probably) find 8 cross-polarized vertically stacked radiating elements, as illustrated in Figure 1. There are two RF input signals per panel, one per polarization, thus each panel acts as two antennas. This is how LTE with 8TX-sectors is deployed: 4 panels with dual polarization per base station.
The picture above shows a real LTE site that I found in Nanjing, China, a couple of years ago. Looking at it from above, the site is structured as illustrated to the right. The site consists of three sectors, each containing a base station with four vertical panels. If you would look inside one of the panels, you will (probably) find 8 cross-polarized vertically stacked radiating elements, as illustrated in Figure 1. There are two RF input signals per panel, one per polarization, thus each panel acts as two antennas. This is how LTE with 8TX-sectors is deployed: 4 panels with dual polarization per base station.