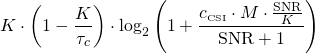Category Archives: Technical insights

Education, Technical insights

Estimating Channels under Channel Hardening

4 Comments

Last year, I wrote a post about channel hardening. To recap, the achievable data rate of a conventional single-antenna channel varies rapidly over time due to the random small-scale fading realizations, and also over frequency due to frequency-selective fading. However, when you have many antennas at the base station and use them for coherent precoding/combining, the fluctuations in data rate average out; we then say that the channel hardens. One follow-up question that I’ve got several times is:

Can we utilize the channel hardening to estimate the channels less frequently?

Unfortunately, the answer is no. Whenever you move approximately half a wavelength, the multi-path propagation will change each element of the channel vector. The time it takes to move such a distance is called a coherence time. This time is the same irrespectively of how many antennas the base station has and, therefore, you still need to estimate the channel once per coherence time. The same applies to the frequency domain, where the coherence bandwidth is determined by the propagation environment and not the number of antennas.

The following flow-chart shows what need to happen in every channel coherence time:

When you get a new realization (at the top of the flow-chart), you compute an estimate (e.g., based on uplink pilots), then you use the estimate to compute a new receive combining vector and transmit precoding vector. It is when you have applied these vectors to the channel that the hardening phenomena appears; that is, the randomness averages out. If you use maximum ratio (MR) processing, then the random realization h1 of the channel vector turns into an almost deterministic scalar channel ||h1||2. You can communicate over the hardened channel with gain ||h1||2 until the end of the coherence time. You then start over again by estimating the new channel realization h2, applying MR precoding/combining again, and then you get ||h2||2 ≈ ||h1||2.

In conclusion, channel hardening appears after coherent combining/precoding has been applied. To maintain a hardened channel over time (and frequency), you need to estimate and update the combining/precoding as often as you would do for a single-antenna channel. If you don’t do that, you will gradually lose the array gain until the point where the channel and the combining/precoding are practically uncorrelated, so there is no array gain left. Hence, there is more to lose from estimating channels too infrequently in Massive MIMO systems than in conventional systems. This is shown in Fig. 10 in a recent measurement paper from Lund University, where you see how the array gain vanishes with time. However, the Massive MIMO system will never be worse than the corresponding single-antenna system.

Commentary, Education, Technical insights

When Normalization is Dangerous

17 Comments

The signal-to-noise ratio (SNR) generally depends on the transmit power, channel gain, and noise power:

Since the spectral efficiency (bit/s/Hz) and many other performance metrics of interest depend on the SNR, and not the individual values of the three parameters, it is a common practice to normalize one or two of the parameters to unity. This habit makes it easier to interpret performance expressions, to select reasonable SNR ranges, and to avoid mistakes in analytical derivations.

There are, however, situations when the absolute value of the transmitted/received signal power matters, and not the relative value with respect to the noise power, as measured by the SNR. In these situations, it is easy to make mistakes if you use normalized parameters. I see this type of errors far too often, both as a reviewer and in published papers. I will give some specific examples below, but I won’t tell you who has made these mistakes, to not point the finger at anyone specifically.

Wireless energy transfer

Electromagnetic radiation can be used to transfer energy to wireless receivers. In such wireless energy transfer, it is the received signal energy that is harvested by the receiver, not the SNR. Since the noise power is extremely small, the SNR is (at least) a billion times larger than the received signal power. Hence, a normalization error can lead to crazy conclusions, such as being able to transfer energy at a rate of 1 W instead of 1 nW. The former is enough to keep a wireless transceiver on continuously, while the latter requires you to harvest energy for a long time period before you can turn the transceiver on for a brief moment.

Energy efficiency

The energy efficiency (EE) of a wireless transmission is measured in bit/Joule. The EE is computed as the ratio between the data rate (bit/s) and the power consumption (Watt=Joule/s). While the data rate depends on the SNR, the power consumption does not. The same SNR value can be achieved over a long propagation distance by using high transmit power or over a short distance by using a low transmit power. The EE will be widely different in these cases. If a “normalized transmit power” is used instead of the actual transmit power when computing the EE, one can get EEs that are one million times smaller than they should be. As a rule-of-thumb, if you compute things correctly, you will get EE numbers in the range of 10 kbit/Joule to 10 Mbit/Joule.

Noise power depends on the bandwidth

The noise power is proportional to the communication bandwidth. When working with a normalized noise power, it is easy to forget that a given SNR value only applies for one particular value of the bandwidth.

Some papers normalize the noise variance and channel gain, but then make the SNR equal to the unnormalized transmit power (measured in W). This may greatly overestimate the SNR, but the achievable rates might still be in the reasonable range if you operate the system in an interference-limited regime.

Some papers contain an alternative EE definition where the spectral efficiency (bit/s/Hz) is divided by the power consumption (Joule/s). This leads to the alternative EE unit bit/Joule/Hz. This definition is not formally wrong, but gives the misleading impression that one can multiply the EE value with any choice of bandwidth to get the desired number of bit/Joule. That is not the case since the SNR only holds for one particular value of the bandwidth.

Knowing when to normalize

In summary, even if it is convenient to normalize system parameters in wireless communications, you should only do it if you understand when normalization is possible and when it is not. Otherwise, you can make embarrassing mistakes, such as submitting a paper where the results are six orders of magnitude wrong. And, unfortunately, there are several such papers that have been published and these create a bad circle by tricking others into making the same mistakes.

5G, Commentary, Technical insights

Further Differences Between Massive MIMO for Sub-6 GHz and mmWave

2 Comments

One of the most read posts on this blog is Six differences between Massive MIMO for sub-6 GHz and mmWave, where we briefly outlined the key differences between how the Massive MIMO technology would be implemented and utilized in different frequency bands. Motivated by the great feedback and interest in this topic, we joined forces with Liesbet Van der Perre and Stefano Buzzi to write a full-length magazine article. It has recently been submitted to IEEE Wireless Communications and a pre-print can be found on ArXiv.org:

Massive MIMO in Sub-6 GHz and mmWave: Physical, Practical, and Use-Case Differences

Commentary, Education, Technical insights

How Distortion from Nonlinear Massive MIMO Transceivers is Radiated Spatially

2 Comments

While the research literature is full of papers that design wireless communication systems under constraints on the maximum transmitted power, in practice, it might be constraints on the equivalent isotropically radiated power (EIRP) or the out-of-band radiation that limit the system operation.

Christopher Mollén recently defended his doctoral thesis entitled High-End Performance with Low-End Hardware: Analysis of Massive MIMO Base Station Transceivers. In the following video, he explains the basics of how the non-linear distortion from Massive MIMO transceivers is radiated in space.

5G, Commentary, Technical insights

A Basic Way to Quantify the Massive MIMO Gain

21 Comments

Several people have recently asked me for a simple way to quantify the spectral efficiency gains that we can expect from Massive MIMO. In theory, going from 4 to 64 antennas is just a matter of changing a parameter value. However, many practical issues need be solved to bring the technology into reality and the solutions might only be developed if we can convince ourselves that the gains are sufficiently large.

While there is no theoretical upper limit on how spectrally efficient Massive MIMO can become when adding more antennas, we need to set some reasonable first goals.  Currently, many companies are trying to implement analog beamforming in a cost-efficient manner. That will allow for narrow beamforming, but not spatial multiplexing.

By following the methodology in Section 3.3.3 in Fundamentals of Massive MIMO, a simple formula for the downlink spectral efficiency is:

(1)   \begin{equation*}K \cdot \left( 1 - \frac{K}{\tau_c} \right) \cdot \log_2 \left( 1+ \frac{ c_{ \textrm{\tiny CSI}} \cdot M \cdot \frac{\mathrm{SNR}}{K}}{\mathrm{SNR}+ 1} \right)\end{equation*}

where $M$ is the number of base-station antennas, $K$ is the number of spatially multiplexed users, $c_{ \textrm{\tiny CSI}} \in [0,1]$ is the quality of the channel estimates, and $\tau_c$ is the number of channel uses per channel coherence block. For simplicity, I have assumed the same pathloss for all the users. The variable $\mathrm{SNR}$ is the nominal signal-to-noise ratio (SNR) of a user,  achieved when $M=K=1$. Eq. (1) is a rigorous lower bound on the sum capacity, achieved under the assumptions of maximum ratio precoding, i.i.d. Rayleigh fading channels, and equal power allocation. With better processing schemes, one can achieve substantially higher performance.

To get an even simpler formula, let us approximate (1) as

(2)   \begin{equation*}K \log_2 \left( 1+ \frac{ c_{ \textrm{\tiny CSI}} M}{K} \right)\end{equation*}

by assuming a large channel coherence and negligible noise.

What does the formula tell us?

If we increase $M$ while $K$ is fixed , we will observe a logarithmic improvement in spectral efficiency. This is what analog beamforming can achieve for $K=1$ and, hence, I am a bit concerned that the industry will be disappointed with the gains that they will obtain from such beamforming in 5G.

If we instead increase $M$ and $K$ jointly, so that  $M/K$ stays constant, then the spectral efficiency will grow linearly with the number of users. Note that the same transmit power is divided between the $K$ users, but the power-reduction per user is compensated by increasing the array gain $M$ so that the performance per user remains the same.

The largest gains come from spatial multiplexing

To give some quantitative numbers, consider a baseline system with $M=4$ and $K=1$ that achieves 2 bit/s/Hz. If we increase the number of antennas to $M=64$, the spectral efficiency will become 5.6 bit/s/Hz. This is the gain from beamforming. If we also increase the number of users to $K=16$ users, we will get 32 bit/s/Hz. This is the gain from spatial multiplexing. Clearly, the largest gains come from spatial multiplexing and adding many antennas is a necessary way to facilitate such multiplexing.

This analysis has implicitly assumed full digital beamforming. An analog or hybrid beamforming approach may achieve most of the array gain for $K=1$. However, although hybrid beamforming allows for spatial multiplexing, I believe that the gains will be substantially smaller than with full digital beamforming.

Education, Technical insights

Are Link Simulations Needed Anymore?

5 Comments

One reason for why capacity lower bounds are so useful is that they are accurate proxies for link-level performance with modern coding. But this fact, well known to information and coding theorists, is often contested by practitioners. I will discuss some possible reasons for that here.

The recipe is to compute the capacity bound, and depending on the code blocklength, add a dB or a few, to the required SNR. That gives the link performance prediction. The coding literature is full of empirical results, showing how far from capacity a code of a given block length is for the AWGN channel, and this gap is usually not extremely different for other channel models – although, one should always check this.

But there are three main caveats with this:

  1. First, the capacity bound, or the “SINR” that it often contains, must be information-theoretically correct. A great deal of papers get this wrong. Emil explained in his blog post last week some common errors. The recommended approach is to map the channel onto one of the canonical cases in Figure 2.9 in Fundamentals of Massive MIMO, verify that the technical conditions are satisfied, and use the corresponding formula.
  2. When computing expressions of the type E[log(1+”SINR”)], then the average should be taken over all quantities that are random within the duration of a codeword. Typically, this means averaging over the randomness incurred by the noise, channel estimation errors, and in many cases the small-scale fading. All other parameters must be kept fixed. Typically, user positions, path losses, shadow fading, scheduling and pilot assignments, are fixed, so the expectation is conditional on those. (Yet, the interference statistics may vary substantially, if other users are dropping in and out of the system.) This in turn means that many “drops” have to be generated, where these parameters are drawn at random, and then CDF curves with respect to that second level of randomness needs be computed (numerically).Think of the expectation E[log(1+”SINR”)] as a “link simulation”. Every codeword sees many independent noise realizations, and typically small-scale fading realizations, but the same realization of the user positions. Also, often, neat (and tight) closed-form bounds on E[log(1+”SINR”)] are available.
  3. Care is advised when working with relatively short blocks (less than a few hundred bits) and at rates close to the constrained capacity with the foreseen modulation format. In this case, many of the “standard” capacity bounds become overoptimistic.As a rule of thumb, compare the capacity of an AWGN channel with the constrained capacity of the chosen modulation at the spectral efficiency of interest, and if the gap is small, the capacity bounds will be useful. If not, then reconsider the choice of modulation format! (See also homework problem 1.4.)

How far are the bounds from the actual capacity typically? Nobody knows, but there are good reasons to believe they are extremely close. Here (Figure 1) is a nice example that compares a decoder that uses the measured channel likelihood, instead of assuming a Gaussian (which is implied by the typical bounding techniques). From correspondence with one of the authors: “The dashed and solid lines are the lower bound obtained by Gaussianizing the interference, while the circles are the rate achievable by a decoder exploiting the non-Gaussianity of the interference, painfully computed through days-long Monte-Carlo. (This is not exactly the capacity, because the transmit signals here are Gaussian, so one could deviate from Gaussian signaling and possibly do slightly better — but the difference is imperceptible in all the experiments we’ve done.)”

Concerning Massive MIMO and its capacity bounds, I have met for a long time with arguments that these capacity formulas aren’t useful estimates of actual performance. But in fact, they are: In one simulation study we were less than one dB from the capacity bound by using QPSK and a standard LDPC code (albeit with fairly long blocks). This bound accounts for noise and channel estimation errors. Such examples are in Chapter 1 of Fundamentals of Massive MIMO, and also in the ten-myth paper:

(I wrote the simulation code, and can share it, in case anyone would want to reproduce the graphs.)

So in summary, while capacity bounds are sometimes done wrong; when done right they give pretty good estimates of actual link performance with modern coding.

(With thanks to Angel Lozano for discussions.)