The channel fading in traditional frequency bands (below 6 GHz) is often well described by the Rayleigh fading model, at least in non-line-of-sight scenarios. This model says that the channel coefficient between any transmit antenna and receive antenna is complex Gaussian distributed, so that its magnitude is Rayleigh distributed.
If there are multiple antennas at the transmitter and/or receiver, then it is common to assume that different pairs of antennas are subject to independent and identically distributed (i.i.d.) fading. This model is called i.i.d. Rayleigh fading and dominates the academic literature to such an extent that one might get the impression that it is the standard case in practice. However, it is rather the other way around: i.i.d. Rayleigh fading only occurs in very special cases in practice, such as having a uniform linear array with half-wavelength-spaced isotropic antennas that is deployed in a rich scattering environment where the multi-paths are uniformly distributed in all directions. If one would remove any of these very specific assumptions then the channel coefficients will become mutually correlated. I covered the basics of spatial correlation in a previous blog post.
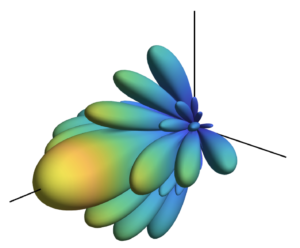
In reality, the channel fading will always be correlated
Some reasons for this are: 1) planar arrays exhibit correlation along the diagonals, since not all adjacent antennas can be half-wavelength-spaced; 2) the antennas have non-isotropic radiation patterns; 3) there will be more multipath components from some directions than from other directions.
With this in mind, I have dedicated a lot of my work to analyzing MIMO communications with correlated Rayleigh fading. In particular, our book “Massive MIMO networks” presents a framework for analyzing multi-user MIMO systems that are subject to correlated fading. When we started the writing, I thought spatial correlation was a phenomenon that was important to cover to match reality but would have a limited impact on the end results. I have later understood that spatial correlation is fundamental to understand how communication systems work. In particular, the modeling of spatial correlation changes the game when it comes to pilot contamination: it is an entirely negative effect under i.i.d. Rayleigh fading models, while a proper analysis based on spatial correlation reveals that one can sometimes benefit from purposely assigning the same pilots to users and then separate them based on their spatial correlation properties.
Future applications for spatial correlation models
The book “Massive MIMO networks” presents a framework for channel estimation and computation of achievable rates with uplink receive combining and downlink precoding for correlated Rayleigh fading channels. Although the title of the book implies that it is about Massive MIMO, the results apply to many beyond-5G research topics. Let me give two concrete examples:
- Cell-free Massive MIMO: In this topic, many geographically distributed access points are jointly serving all the users in the network. This is essentially a single-cell Massive MIMO system where the access points can be viewed as the distributed antennas of a single base station. The channel estimation and computation of achievable rates can be carried out as described “Massive MIMO networks”. The key differences are instead related to which precoding/combining schemes that are considered practically implementable and the reuse of pilots within a cell (which is possible thanks to the strong spatial correlation).
- Extremely Large Aperture Arrays: There are other names for this category, such as holographic MIMO, large intelligent surfaces, and ultra-massive MIMO. The new terminologies are used to indicate the use of co-located arrays that are much larger (in terms of the number of antennas and the physical size) than what is currently considered by the industry when implementing Massive MIMO in 5G. In this case, the spatial correlation matrices must be computed differently than described in “Massive MIMO networks”, for example, to take near-field effects and shadow fading variations into consideration. However, once the spatial correlation matrices have been computed, then the same framework for channel estimation and computation of achievable rates is applicable.
The bottom line is that we can analyze many new exciting beyond-5G technologies by making use of the analytical frameworks developed in the past decade. There is no need to reinvent the wheel but we should reuse as much as possible from previous research and then focus on the novel components. Spatial correlation is something that we know how to deal with and this must not be forgotten.