Line-of-sight channels normally contain many propagation paths, whereof one is the direct path and the others are paths were the signals are scattered on different objects. The interaction between these paths lead to fading phenomena, which is often modeled statistically using Rician fading (sometimes written as Ricean fading). The main assumption is that the complex-valued channel coefficient 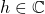 in the complex baseband can be divided into two parts:
in the complex baseband can be divided into two parts:
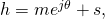
where 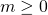 is the magnitude of the direct path between the transmitter and receiver and
is the magnitude of the direct path between the transmitter and receiver and ![Rendered by QuickLaTeX.com \theta \in [0,2\pi]](https://ma-mimo.ellintech.se/wp-content/ql-cache/quicklatex.com-e70126963911574a22ab8afc7da04ca9_l3.png) is the corresponding phase shift. The second part,
is the corresponding phase shift. The second part,  , represents all the scattered paths. This part is separated from the direct path since it consists of many paths, each being of roughly the same strength but substantially weaker than the direct path. It is modeled by Rayleigh fading, which implies
, represents all the scattered paths. This part is separated from the direct path since it consists of many paths, each being of roughly the same strength but substantially weaker than the direct path. It is modeled by Rayleigh fading, which implies 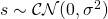 . The complex Gaussian distribution is motivated by the central limit theorem, which says that the sum of many independent and identically distributed random variables is approximately Gaussian.
. The complex Gaussian distribution is motivated by the central limit theorem, which says that the sum of many independent and identically distributed random variables is approximately Gaussian.
Under these assumptions, the magnitude 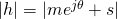 of the channel coefficient is Rice/Rician distributed, which is why it is called Rician fading. More precisely,
of the channel coefficient is Rice/Rician distributed, which is why it is called Rician fading. More precisely, 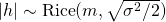 , which depends on the magnitude
, which depends on the magnitude 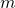 and the variance
and the variance 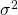 of the scattering.
of the scattering.
Interestingly, the distribution does not depend on the phase 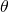 , because the magnitude removes phases and
, because the magnitude removes phases and  and
and 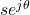 are equally distributed. Hence, it is common to omit
are equally distributed. Hence, it is common to omit 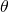 in the performance analysis of Rician fading channels. As long as the channel is perfectly known at the receiver, it will not make any difference when quantifying the SNR or capacity.
in the performance analysis of Rician fading channels. As long as the channel is perfectly known at the receiver, it will not make any difference when quantifying the SNR or capacity.
The common misunderstanding
We cannot neglect the phase 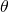 when analyzing practical systems where the receiver needs to estimate the channel. The value of
when analyzing practical systems where the receiver needs to estimate the channel. The value of 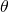 varies at the same pace as
varies at the same pace as  , and for exactly the same reason: The transmitter or receiver moves, which induces small phase shifts in every path. Since
, and for exactly the same reason: The transmitter or receiver moves, which induces small phase shifts in every path. Since  contains a large number of paths with approximately the same magnitude but random phases, the sum of the many terms with random phases give rise to the Gaussian distribution. The phase-shift of the direct path must be treated separately since this path is substantially stronger.
contains a large number of paths with approximately the same magnitude but random phases, the sum of the many terms with random phases give rise to the Gaussian distribution. The phase-shift of the direct path must be treated separately since this path is substantially stronger.
Unfortunately, my experience is that the vast majority of paper on Rician fading channels ignores this fact by simply treating 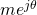 as a deterministic constant that is perfectly known at the receiver. I have done this myself in several papers, including this one from 2010 that has received 200+ citations. Unfortunately, the results obtained with that simplified model are practically questionable. If we don’t know
as a deterministic constant that is perfectly known at the receiver. I have done this myself in several papers, including this one from 2010 that has received 200+ citations. Unfortunately, the results obtained with that simplified model are practically questionable. If we don’t know  in advance, how can we know
in advance, how can we know 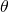 ? At best, the results obtained with a perfectly known
? At best, the results obtained with a perfectly known 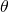 can be interpreted as an upper bound on what is practically achievable.
can be interpreted as an upper bound on what is practically achievable.
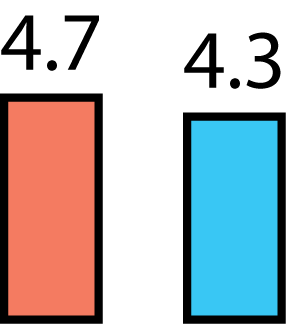
We analyzed the importance of correctly modeled random phases in a recent paper on cell-free massive MIMO. We compared the performance when using an ideal phase-aware MMSE estimator and a phase-unaware LMMSE estimator. The spectral efficiency loss due to a lack of knowing 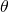 ranges from 2% to 50% in different simulations, depending on the pilot length and interference situation. Hence, there are cases where it is very important to know the phase correctly.
ranges from 2% to 50% in different simulations, depending on the pilot length and interference situation. Hence, there are cases where it is very important to know the phase correctly.