In this post I propose a new type of moveable antenna that I call the Holographic Spinning Antenna (HSA), a concept where an antenna is spun at extremely high rates, which appears novel with no previous published work. This spinning antenna could fit into the trend of reconfigurable components in RF systems such as reconfigurable intelligent surfaces, moveable, rotatable and fluid antennas. Whether this spinning antenna is physically feasible, and even then, brings any additional benefit, remains to be answered. I describe the HSA and contribute with a toy example below.
Background
Some time ago the YouTube algorithm recommended me a commercial for a “Holographic Led Fan” (HLF), which exists under other names such as “holographic fan display” etc. A HLF consists of an axis driven by an electrical motor, on which at least one arm with a 1-dimensional LED stripe is mounted. Like a fan, but the blades are LED stripes instead. When the fan is turned off, but the LED is on, you see a 1D stripe of lights. When you turn on the fan and it spins sufficiently fast, because of the retinal persistence of our eyes, the LEDs are blurred by motion through space and we see a floating 2D image instead of the 1D stripes.
If you work with wireless communications these 1D LED stripes could induce some déjà vu: The LED elements look quite like planar antenna elements and the arms of the HLF look like a uniform linear array (ULA). My question is: Is there an equivalent effect of spinning a ULA sufficiently fast?
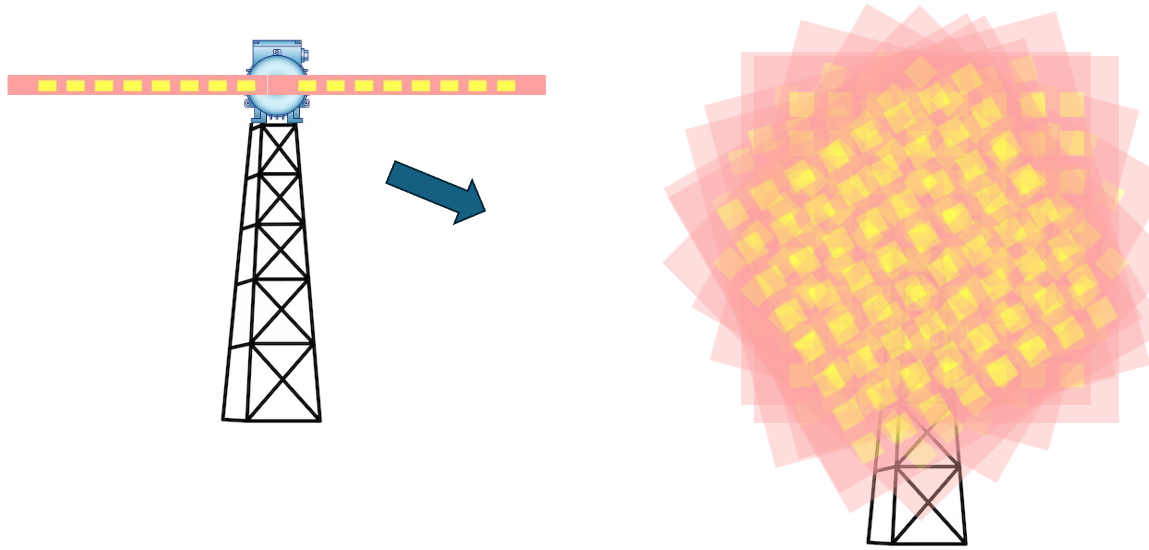
Can we transmit more information if an antenna is spun sufficiently fast? Clearly, spinning the LEDs creates a new degree of freedom (angle) which can encode a 2D image.
To keep it simple I will consider block fading, and my idea is that “sufficiently fast” is at least 2 revolutions per channel coherence time. I doubt this is fast enough to cause any effect of persistence in the antennas, but it can still lead to interesting questions. I start with a conceptual description first and then a toy example.
Conceptual Description
Under the idealistic assumptions of block fading, the idea is to transmit or receive pilots the first revolution, then to transmit or receive data over the same channel instance the second revolution. In this way, you increase the channel diversity in a coherence block, but the trade-off is lower SNR. Of course, if you have multiple antennas symmetrically placed on the disc (as in the figure below) you can spin half a revolution and then transmit half a revolution, which would allow for lower RPM. Compared to the “windmill” above, I suggest a slightly more feasible construction below:
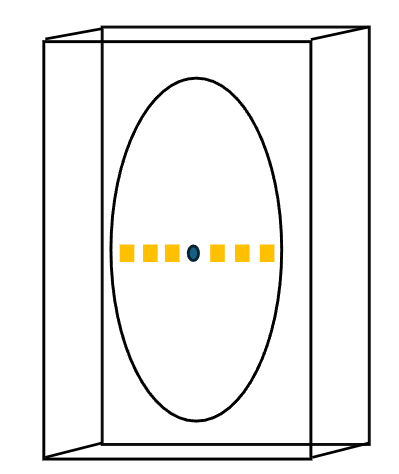
In this construction I envision 5 main components:
- A circular disc.
- At least 1 antenna on the disc. In the illustration there are 6 antennas placed symmetrically, 3 on each side of the disc.
- A way to spin the disc extremely fast. Maybe in a capsule of vacuum and some maglev technique? See also flywheel energy storage.
- A way to read and write the signals of the antennas on the spinning disc.
- A way to power the antennas on the spinning disc.
It has been demonstrated that one can spin a compact disc (CD) up to 25 000 RPM, which is 2.4 milliseconds per revolution. I will not delve into the physics of spinning discs for now and instead refer to the MythBusters as evidence:
Toy Example
Assume Rayleigh block fading, coherence time is ![]() discrete symbols, data and additive noise are normalized complex Gaussian:
discrete symbols, data and additive noise are normalized complex Gaussian: ![]() . We consider a single antenna and compare the HSA spinning case against the typical static case.
. We consider a single antenna and compare the HSA spinning case against the typical static case.
Note that the toy example is similar to a switched array, but the spinning antenna is fundamentally different in that you can also transmit/receive continuously in space and not just at the discrete antenna locations in a switched array.
Static antenna
In the static case we have a single antenna fixed in space, depicted below.

At ![]() the channel
the channel ![]() is estimated perfectly. At remaining
is estimated perfectly. At remaining ![]() symbols you transmit/receive the same symbol of data
symbols you transmit/receive the same symbol of data ![]() over the same channel instance
over the same channel instance ![]() :
:
(1) ![]()
s.t.
(2) ![]()
where ![]() . Then apply MR combining with
. Then apply MR combining with ![]() to the input
to the input
(3) ![]()
where
(4) ![]()
giving rate
(5) ![]()
and outage probability
(6) ![]()
which has a closed form expression, excluded here.
Spinning antenna
In the spinning case we have an antenna on a rotating disc. For the first ![]() symbols you estimate
symbols you estimate ![]() independent channel instances perfectly. The last
independent channel instances perfectly. The last ![]() symbols you transmit/receive the same symbol of data over each channel.
symbols you transmit/receive the same symbol of data over each channel.
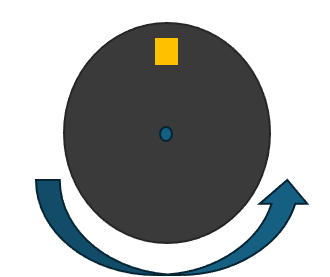
Note that the assumption of ![]() independent channels necessitates that the points of measurement are separated by
independent channels necessitates that the points of measurement are separated by ![]() , which in turn means the maximum wavelength is two times the disc diameter. In the spinning case the channel
, which in turn means the maximum wavelength is two times the disc diameter. In the spinning case the channel ![]() is new for each of the final
is new for each of the final ![]() measurements:
measurements:
(7) ![]()
With MR combining as previously, one gets
(8) 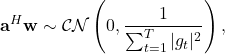
with rate
(9) 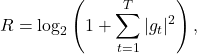
and outage probability
(10) ![]()
Simulation results
I simulate ![]() using 1000 monte-carlo trials, and compute the probability of outage
using 1000 monte-carlo trials, and compute the probability of outage ![]() numerically with
numerically with ![]() . We see that the spinning antenna gets a much lower probability of outage for
. We see that the spinning antenna gets a much lower probability of outage for ![]() than the static if
than the static if ![]() is sufficiently high. However, the static has a higher expected rate, although with higher variance in rate than the spinning antenna.
is sufficiently high. However, the static has a higher expected rate, although with higher variance in rate than the spinning antenna.
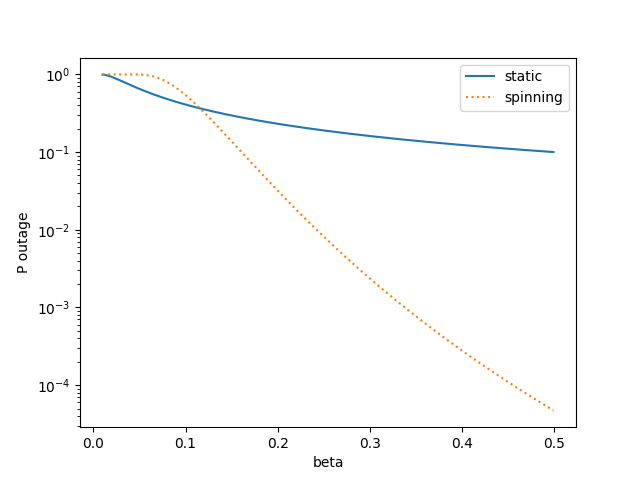
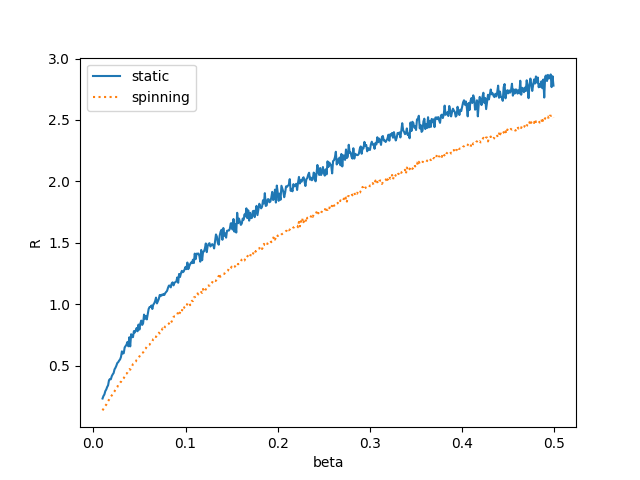
The take-away is that the static antenna has a higher rate on average, but if you want stronger guarantees on your rate the spinning antenna could be a better choice.
Multi-antenna case
I believe you can find additional interesting things you if you assume two symmetrically placed antennas, comparing the static and spinning case. For example, in the spinning case you can effectively beamform in 2 dimensions using only 2 antennas, which you cannot do in the static case.
Optimal power control
If average power is limited per coherence block, in the spinning case you should get some water filling problem where you want to spend most power on the best channels, which you wont get in the static case.
Summary
I propose the “Holographic Spinning Antenna”, which is an antenna that spins extremely fast (compared to traditional spinning antennas such as radar). From my minimal toy example and simulation results I suggest that the spinning antenna has a lower probability of outage, but not necessarily a higher ergodic rate compared to the static antenna. The HSA could be physically possible if it is the size of a CD and could be used for wavelengths up to 120*2 millimeters.
I would say there are two main questions to be answered:
- Does the HSA have any significant benefit compared to a static/switched array motivating the added physical complexity of spinning the antenna?
- Is the HSA physically possible?
I encourage anyone curious enough to keep exploring the concept of a spinning antenna under better assumptions and models.
Finally, thanks to Emil Björnson and my main supervisor Erik G. Larsson for letting me post this in the blog, and for letting me entertain my idea of a spinning antenna.
Have a great new year,
Martin Dahl,
PhD Student at Linköping University,
Department of Electrical Engineering (ISY),
Division of Communication Systems (CommSys),
martin.dahl@liu.se


