Beyond 5G, Commentary, Technical insights

Centralized Versus Distributed Processing in Cell-Free Massive MIMO

6 Comments
A figure from my first paper on Network MIMO, which is nowadays called Cell-Free Massive MIMO.

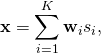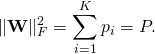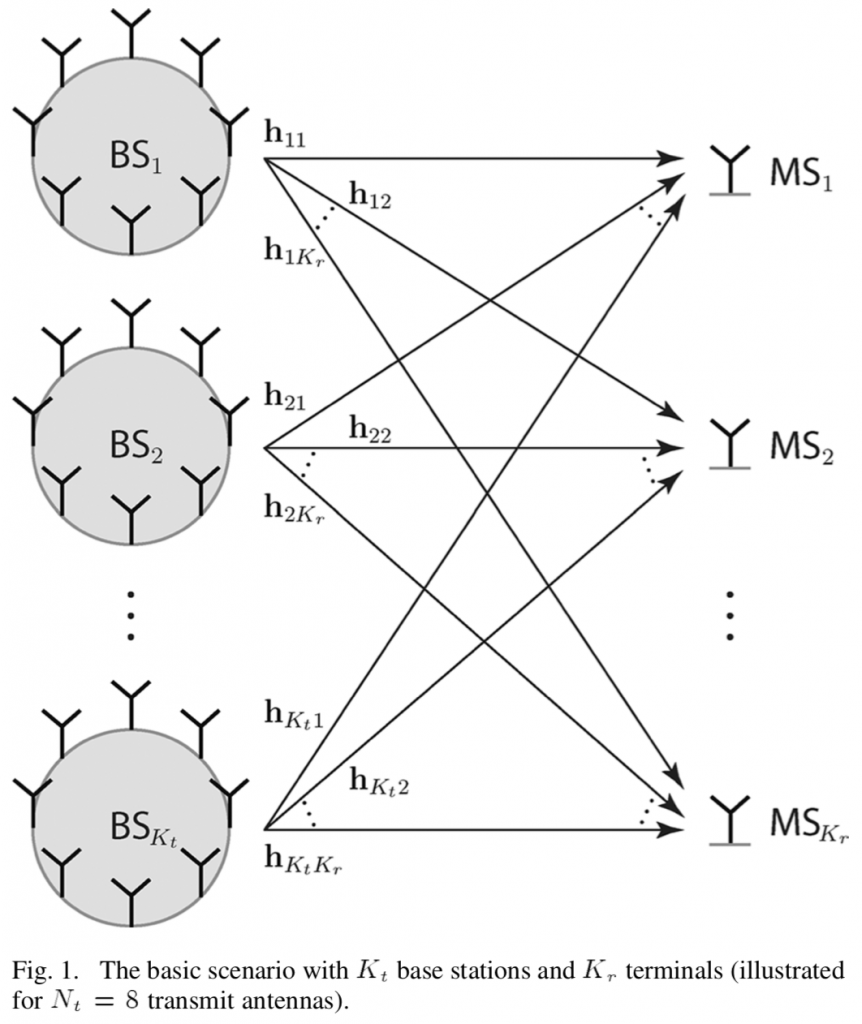
The new Cell-Free Massive MIMO concept has its roots in the classical Network MIMO concept, and has also been given many other names over the years (e.g., coordinated multipoint). When I started my research on the topic in 2009, the standard assumption was that a set of base stations were jointly transmitting to a set of users by sharing both the data signals and their respective channel state information (CSI). In my first journal paper, we showed that one can get away with only sharing the data signals between the base stations because each one only needs local CSI (between itself and the users) to beamform to the users. The price to pay is that the base stations cannot cancel each others’ interference, so each one should preferably have multiple antennas so it can control how much interference it causes. This was my first well-cited paper but, to be honest, I am still not sure how significant results are.

On the one hand, it is very convenient to only utilize local CSI at every base station, because it can be estimated from uplink pilots in a TDD system, which was a key motivation behind our 2010 paper. The time-critical precoding computation can then be initiated immediately after the pilots have been received, instead of waiting for the CSI to be shared between the base stations. This property was later utilized in the first Cell-Free Massive MIMO papers [Ngo, Nayebi] to alleviate the need for sharing CSI.

On the other hand, CSI is usually a small fraction of the signaling between a base station and the rest of the system in Network MIMO. The majority of the signaling consists of the data signals; for example, if a coherence block with 200 channel uses consists of 20 pilot symbols and 180 data symbols, then there is 180/20 = 9 times more data than CSI. Interestingly, our recent paper “Making Cell-Free Massive MIMO Competitive With MMSE Processing and Centralized Implementation” shows that if Cell-Free Massive MIMO is implemented by sending all CSI to an edge-cloud processor that takes care of all the signal processing, both the communication performance and the signaling load can be greatly improved as compared to the fully distributed approach (which was considered in my 2010 paper and then became the standard assumption in the Cell-Free Massive MIMO literature).

The bottom line is that it is hard to make a distributed network implementation competitive compared to a centralized one. Unless we can find a really clever implementation, there is a risk that we lose too much in communication performance and also raise the fronthaul capacity requirements.

5G, Technical insights

Is the Pathloss Larger at mmWave Frequencies?

10 Comments

The range of mmWave communication signals is often said to be lower than for signals in the conventional sub-6 GHz bands. This is usually also the case but the reason for it might not be the one that you think. I will explain what I mean in this blog post.

If one takes a look at the classical free-space pathloss formula, the received power P_r is

(1)   \begin{equation*}P_r = P_t \left( \frac{\lambda}{4\pi d} \right)^2,\end{equation*}

where the transmit power is denoted by P_t, the wavelength is \lambda, and the propagation distance is d. This formula shows that the received power is proportional to the wavelength and, thus, will be smaller when we increase the carrier frequency; that is, the received power is lower at 60 GHz (\lambda=5 mm) than at 3 GHz (\lambda=10 cm). But there is an important catch: the dependence on \lambda is due to the underlying assumption of having a receive antenna with the effective area

(2)   \begin{equation*}A = \frac{\lambda^2}{4\pi}.\end{equation*}

Hence, if we consider a receive antenna with arbitrary effective area A, we can instead write the received signal in (1) as

(3)   \begin{equation*}P_r = P_t \frac{A}{4\pi d^2},\end{equation*}

which is frequency-independent as long as we keep the antenna area A fixed as we change the carrier frequency. Since the area of a fixed-gain antenna actually is proportional to \lambda^2, as exemplified in (2), in practice we will need to use arrays of multiple antennas in mmWave bands to achieve the same total antenna area A as in lower bands. This is what is normally done in mmWave communications for cellular networks, while a single high-gain antenna with large area can be used for fixed links (e.g., backhaul between base stations or between a satellite and ground station). As explained in Section 7.5 of Massive MIMO Networks, one can actually play with the antenna areas at both the transmitter and receiver to keep the same pathloss in the mmWave bands, while actually reducing the total antenna area!

So why is the signal range shorter in mmWave bands?

The main reasons for the shorter range are:

  • Larger propagation losses in non-line-of-sight scenarios, for example, due to less scattering (fewer propagation paths) and larger penetration losses.
  • The use more bandwidth, which leads to lower SNR.

Edit: The atmospheric, molecular, and rain attenuation losses are larger in some mmWave bands, but it is primarily a concern for macro cells with ranges measured in kilometers (see Figures 2-3 in this paper).

Beyond 5G, News

Multiple Antenna Technologies for Beyond 5G

Leave a comment

I am one of the guest editors of the JSAC special issue on “Multiple Antenna Technologies for Beyond 5G” which had its submission deadline on October 1. We received 133 submissions that span emerging topics such as Cell-free Massive MIMO, intelligent reflective surfaces, terahertz communications, new hardware architectures (e.g., lens arrays), and index modulation. It will take a lot of hard work to review all these submissions, but I am convinced that the selected papers will be of high quality and present a range of interesting concepts that can be utilized in beyond 5G systems.

In addition to the technical papers, the guest editors have also written a survey paper that has the same name as the special issue. A draft of it is available on arXiv. This paper describes the state-of-the-art and open problems related to several of the topics described above.

Commentary, Technical insights

How to Normalize a Precoding Matrix?

18 Comments

The transmitted signal \mathbf{x} from an M-antenna base station can consist of multiple information signals that are transmitted using different precoding (e.g., different spatial directivity). When there are K unit-power data signals s_1,\ldots,s_K intended for K different users, the transmitted signal can be expressed as

(1)   \begin{equation*}\mathbf{x} = \sum_{i=1}^{K} \mathbf{w}_i s_i,\end{equation*}

where \mathbf{w}_1,\ldots,\mathbf{w}_K are the M-dimensional precoding vectors assigned to the different users. The direction of the vector \mathbf{w}_i determines the spatial directivity of the signal s_i, while the squared norm \|\mathbf{w}_i\|^2 determines the associated transmit power. Massive MIMO usually means that M\gg K.

When selecting the precoding vectors, we need to make sure that we are not using too much transmit power. If the maximum power is P and we define the M \times K precoding matrix

(2)   \begin{equation*} \mathbf{W} = [\mathbf{w}_1 \, \, \ldots \,\, \mathbf{w}_K],\end{equation*}

then we need to make sure that the squared Frobenius norm of \mathbf{W} equals the maximum transmit power:

(3)   \begin{equation*} \| \mathbf{W} \|_F^2 = P.\end{equation*}

In the Massive MIMO literature, there are two popular methods to achieve that: matrix normalization and vector normalization. The papers [Ref1], [Ref2] consider both methods, while other papers only consider one of the methods. The main idea is to start from an arbitrarily selected precoding matrix \mathbf{F} = [\mathbf{f}_1 \, \, \ldots \,\, \mathbf{f}_K] and then adapt it to satisfy the power constraint in (3).

Matrix normalization: In this case, we take the matrix \mathbf{F} and scales all the entries with the same number, which is selected to satisfy (3). More precisely, we select

(4)   \begin{equation*}\mathbf{W} = \frac{\sqrt{P}}{\|\mathbf{F} \|_F} \mathbf{F}.\end{equation*}

Vector normalization: In this case, we first normalize each column in \mathbf{F} to have unit norm and then scale them all with \sqrt{P/K} to satisfy (3). More precisely, we select

(5)   \begin{equation*}\mathbf{W} = \sqrt{\frac{P}{K}} \left[ \frac{\mathbf{f}_1}{\| \mathbf{f}_1\|} \, \, \ldots \,\, \frac{\mathbf{f}_K}{\| \mathbf{f}_K\|} \right].\end{equation*}

Which of the two normalizations should be used?

This is a question that I receive now and then, so I wrote this blog post to answer it once and for all. My answer: none of them!

The problem with matrix normalization is that the method that was used to select \mathbf{F} will determine how the transmit power is allocated between the different signals/users. Hence, we are not in control of the power allocation and we cannot fairly compare different precoding schemes. For example, maximum-ratio (MR) allocates more power to users with strong channels than users with weak channels, while zero-forcing (ZF) does the opposite. Hence, if one tries to compare MR and ZF under matrix normalization, the different power allocations will strongly influence the results.

This issue is resolved by vector normalization. However, the problem with vector normalization is that all users are assigned the same amount of power, which is undesirable if some users have strong channels and others have weak channels. One should always make a conscious decision when it comes to power allocation between users.

What we should do instead is to select the precoding matrix as

(6)   \begin{equation*}\mathbf{W} = \left[ \sqrt{p_1} \frac{\mathbf{f}_1}{\| \mathbf{f}_1\|} \, \, \ldots \,\, \sqrt{p_K} \frac{\mathbf{f}_K}{\| \mathbf{f}_K\|} \right],\end{equation*}

where p_1,\ldots,p_K are variables representing the power assigned to each of the users. These should be carefully selected to maximize some performance goals of the network, such as the sum rate, proportional fairness, or max-min fairness. In any case, the power allocation must be selected to satisfy the constraint

(7)   \begin{equation*} \| \mathbf{W} \|_F^2 = \sum_{i=1}^{K} p_i = P.\end{equation*}

There are plenty of optimization algorithms that can be used for this purpose. You can find further details, examples, and references in Section 7.1 of my book Massive MIMO networks.

5G, Commentary, Technical insights

Channel Sparsity in Massive MIMO

10 Comments

Channel estimation is critical in Massive MIMO. One can use the basic least-squares (LS) channel estimator to learn the multi-antenna channel from pilot signals, but if one has prior information about the channel’s properties, that can be used to improve the estimation quality. For example, if one knows the average channel gain, the linear minimum mean-squared error (LMMSE) estimator can be used, as in most of the literature on Massive MIMO.

There are many attempts to exploit further channel properties, in particularly channel sparsity is commonly assumed in the academic literature. I have recently received several questions about this topic, so I will take the opportunity to give a detailed answer. In particular, this blog post discusses temporal and spatial sparsity.

Temporal sparsity

This means that the channel’s impulse response contains one or several pulses with zeros in between. These pulses could represent different paths, in a multipath environment, which are characterized by non-overlapping time delays. This does not happen in a rich scattering environment with many diffuse scatterers having overlapping delays, but it could happen in mmWave bands where there are only a few reflected paths.

If one knows that the channel has temporal sparsity, one can utilize such knowledge in the estimator to determine when the pulses arrive and what properties (e.g., phase and amplitude) each one has. However, several hardware-related conditions need to be satisfied. Firstly, the sampling rate must be sufficiently high so that the pulses can be temporally resolved without being smeared together by aliasing. Secondly, the receiver filter has an impulse response that spreads signals out over time, and this must not remove the sparsity.

Spatial sparsity

This means that the multipath channel between the transmitter and receiver only involves paths in a limited subset of all angular directions. If these directions are known a priori, it can be utilized in the channel estimation to only estimate the properties (e.g., phase and amplitude) in those directions. One way to determine the existence of spatial sparsity is by computing a spatial correlation matrix of the channel and analyze its eigenvalues. Each eigenvalue represents the average squared amplitude in one set of angular directions, thus spatial sparsity would lead to some of the eigenvalues being zero.

Just as for temporal sparsity, it is not necessary that spatial sparsity can be utilized even if it physically exists. The antenna array must be sufficiently large (in terms of aperture and number of antennas) to differentiate between directions with signals and directions without signals. If the angular distance between the channel paths is smaller than the beamwidth of the array, it will smear out the paths over many angles. The following example shows that Massive MIMO is not a guarantee for utilizing spatial sparsity.

The figure below considers a 64-antenna scenario where the received signal contains only three paths, having azimuth angles -20°, +30° and +40° and a common elevation angle of 0°. If the 64 antennas are vertically stacked (denoted 1 x 64), the signal gain seems to be the same from all azimuth directions, so the sparsity cannot be observed at all. If the 64 antennas are horizontally stacked (denoted 64 x 1), the signal gain has distinct peaks at the angles of the three paths, but there are also ripples that could have hidden other paths. A more common 64-antenna configuration is a 8 x 8 planar array, for which only two peaks are visible. The paths 30° and 40° are lumped together due to the limited resolution of the array.

Figure: The received signal gain that is observed from different azimuth angles, using different array geometries. The true signal only contains three paths, which are coming from the azimuth angles -20°, +30° and +40°.

In addition to have a sufficiently high spatial resolution, a phase-calibrated array might be needed to make use of sparsity, since random phase differences between the antennas could destroy the structure.

Do we need sparsity?

There is no doubt that temporal and spatial sparsity exist, but not every channel will have it. Moreover, the transceiver hardware will destroy the sparsity unless a series of conditions are satisfied. That is why one should not build a wireless technology that requires channel sparsity because then it might not function properly for many of the users. Sparsity is rather something to utilize to improve the channel estimation in certain special cases.

TDD-reciprocity based Massive MIMO, as proposed by Marzetta and further considered in my book Massive MIMO networks, does not require channel sparsity. However, sparsity can be utilized as an add-on when available. In contrast, there are many FDD-based frameworks that require channel sparsity to function properly.

Reproduce the results: The code that was used to produce the plot can be downloaded from my GitHub.

5G, Commentary, Technical insights

Massive MIMO Enables Fixed Wireless Access

2 Comments

The largest performance gains from Massive MIMO are achieved when the technology is used for spatial multiplexing of many users. These gains can only be harnessed when there actually are many users that ask for data services simultaneously. I sometimes hear the following negative comments about Massive MIMO:

  1. The data traffic is so bursty that there seldom are more than one or two users that ask for data simultaneously.
  2. When there are multiple users, the uplink SNR is often too poor to get the high quality channel state information that is needed to truly benefit from spatial multiplexing.

These points might indeed be true in current cellular networks, but I believe the situation will change in the future. In particular, the new fixed wireless access services require that the network can simultaneously deliver high-rate services to many customers. The business case for these service rely strongly on Massive MIMO and spatial multiplexing, so that one base station site can guarantee a certain data rate to as many customers as possible (just as fiber and cable connections can). The fixed installation of the customer equipment means that channel state information is much easier to acquire (due to better channel conditions, higher transmit power, and absence of mobility). The following video from Ericsson touches upon some of these aspects:

5G, Beyond 5G, Education, Technical insights

Scalable Cell-Free Massive MIMO

21 Comments

Cell-free massive MIMO is likely one of the technologies that will form the backbone of any xG with x>5. What distinguishes cell-free massive MIMO from distributed MIMO, network MIMO or cooperative multi-point (CoMP)? The short answer is that cell-free massive MIMO works, it can deliver uniformly good service throughout the coverage area, and it requires no prior knowledge of short-term CSI (just like regular cellular massive MIMO). A longer answer is here. The price to pay for this superiority, no shock, is the lack of scalability: for canonical cell-free massive MIMO there is a practical limit on how large the system can be, and this scalability concerns both the power control, the signal processing, and the organization of the backhaul.

At ICC this year we presented this approach towards scalable cell-free massive MIMO. A key insight is that power control is extremely vital for performance, and a scalable cell-free massive MIMO solution requires a scalable power control policy. No surprise, some performance must be sacrificed relative to canonical cell-free massive MIMO. Coincidentally, another paper in the same session (WC-26) also devised a power control policy with similar qualities!

Take-away point? There are only three things that matter for the design of cell-free massive MIMO signal processing algorithms and power control policies: scalability, scalability and scalability…

News – commentary – mythbusting