Cell-free massive MIMO might be one of the core 6G physical layer technologies. One of my students, Giovanni Interdonato, defended his Ph.D. thesis on this topic earlier this week. In this video, he speaks with me about his thesis work and his time as a doctoral student.
Category Archives: Education
Beyond the Cellular Paradigm: Cell-Free Architectures with Radio Stripes
I just finished giving an IEEE Future Networks Webinar on the topic of Cell-free Massive MIMO and radio stripes. The webinar is more technical than my previous popular-science video on the topic, but it can anyway be considered an overview on the basics and the implementation of the technology using radio stripes.
If you missed the chance to view the webinar live, you can access the recording and slides afterwards by following this link. The recording contains 42 minutes of presentation and 18 minutes of Q/A session. If your question was not answered during the session, please feel to ask it here on the blog instead.
Intelligent Reflecting Surfaces: On Use Cases and Path Loss Model
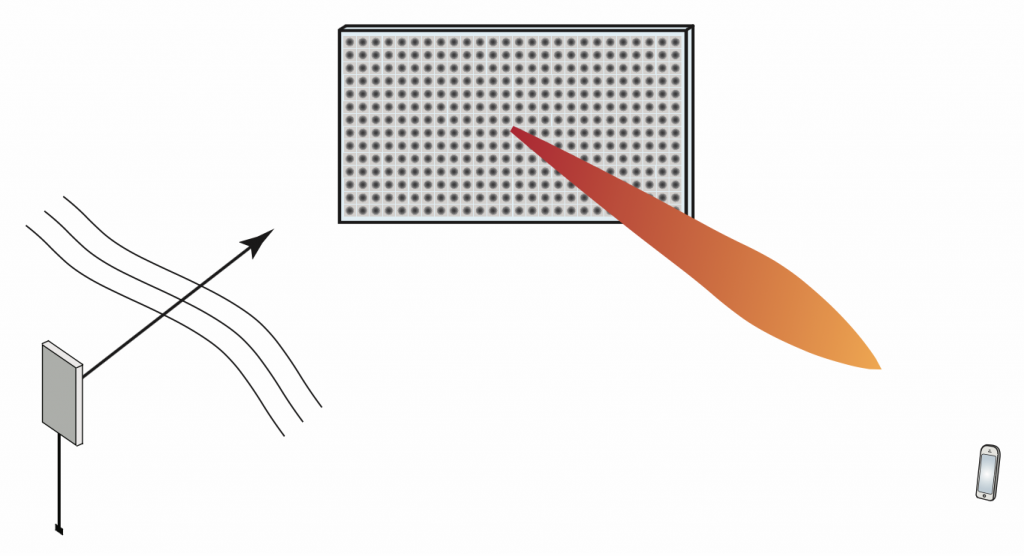
Emerging intelligent reflecting surface (IRS) technology, also known under the names “reconfigurable intelligent surface” and “software-controlled metasurface”, is sometimes marketed as an enabling technology for 6G. How do they work, what are their use cases and how much will they improve wireless access performance at large?
The physical principle of an IRS is that the surface is composed of ![]() atoms, each of which acts as an “intelligent” scatterer: a small antenna that receives and re-radiates without amplification, but with a controllable phase-shift. Typically, an atom is implemented as a small patch antenna terminated with an adjustable impedance. Assuming the phase shifts are properly adjusted, the
atoms, each of which acts as an “intelligent” scatterer: a small antenna that receives and re-radiates without amplification, but with a controllable phase-shift. Typically, an atom is implemented as a small patch antenna terminated with an adjustable impedance. Assuming the phase shifts are properly adjusted, the ![]() scattered wavefronts can be made to add up constructively at the receiver. If coupling between the atoms is neglected, the analysis of an IRS essentially entails (i) finding the Green’s function of the source (a sum of spherical waves if close, or a plane wave if far away), (ii) computing the impinging field at each atom, (iii) integrating this field over the surface of each atom to find a current density, (iv) computing the radiated field from each atom using physical-optics approximation, and (v) applying the superposition principle to find the field at the receiver. If the atoms are electrically small, one can approximate the re-radiated field by pretending the atoms are point sources and then the received “signal” is basically a superposition of phase-shifted (as
scattered wavefronts can be made to add up constructively at the receiver. If coupling between the atoms is neglected, the analysis of an IRS essentially entails (i) finding the Green’s function of the source (a sum of spherical waves if close, or a plane wave if far away), (ii) computing the impinging field at each atom, (iii) integrating this field over the surface of each atom to find a current density, (iv) computing the radiated field from each atom using physical-optics approximation, and (v) applying the superposition principle to find the field at the receiver. If the atoms are electrically small, one can approximate the re-radiated field by pretending the atoms are point sources and then the received “signal” is basically a superposition of phase-shifted (as ![]() ), amplitude-scaled (as
), amplitude-scaled (as ![]() ) source signals.
) source signals.
A point worth re-iterating is that an atom is a scatterer, not a “mirror”. A more subtle point is that the entire IRS as such, consisting of a collection of scatterers, is itself also a scatterer, not a mirror. “Mirrors” exist only in textbooks, when a plane wave is impinging onto an infinitely large conducting plate (none of which exist in practice). Irrespective of how the IRS is constructed, if it is viewed from far enough away, its radiated field will have a beamwidth that is inversely proportional to its size measured in wavelengths.
Two different operating regimes of IRSs can be distinguished:
1. Both transmitter and receiver are in the far-field of the surface. Then the waves seen at the surface can be approximated as planar; the phase differential from the surface center to its edge is less than a few degrees, say. In this case the phase shifts applied to each atom should be linear in the surface coordinate. The foreseen use case would be to improve coverage, or provide an extra path to improve the rank of a point-to-point MIMO channel. Unfortunately in this case the transmitter-IRS-path loss scales very unfavorably, as ![]() where
where ![]() is the number of meta-atoms in the surface, and the reason is that again, the IRS itself acts as a (large) scatterer, not a “mirror”. Therefore the IRS has to be quite large before it becomes competitive with a standard single-antenna decode-and-forward relay, a simple, well understood technology that can be implemented using already widely available components, at small power consumption and with a small form factor. (In addition, full-duplex technology is emerging and may eventually be combined with relaying, or even massive MIMO relaying.)
is the number of meta-atoms in the surface, and the reason is that again, the IRS itself acts as a (large) scatterer, not a “mirror”. Therefore the IRS has to be quite large before it becomes competitive with a standard single-antenna decode-and-forward relay, a simple, well understood technology that can be implemented using already widely available components, at small power consumption and with a small form factor. (In addition, full-duplex technology is emerging and may eventually be combined with relaying, or even massive MIMO relaying.)
2. At least one of the transmitter and the receiver is in the surface near-field. Here the plane-wave approximation is no longer valid. The IRS can then either be sub-optimally configured to act as a “mirror”, in which case the phase shifts vary linearly as function of the surface coordinate. Alternatively, it can be configured to act as a “lens”, with optimized phase-shifts, which is typically better. As shown for example in this paper, in the near-field case the path loss scales more favorably than in the far-field case. The use cases for the near-field case are less obvious, but one can think of perhaps indoor environments with users close to the walls and every wall covered by an IRS. Another potential use case that I learned about recently is to use the IRS as a MIMO transmitter: a single-antenna transmitter near an IRS can be jointly configured to act as a MIMO beamforming array.
So how useful will IRS technology be in 6G? The question seems open. Indoor coverage in niche scenarios, but isn’t this an already solved problem? Outdoor coverage improvement, but then (cell-free) massive MIMO seems to be a much better option? Building MIMO transmitters from a single-antenna seems exciting, but is it better than using conventional RF? Perhaps it is for the Terahertz bands, where implementation of coherent MIMO may prove truly challenging, that IRS technology will be most beneficial.
A final point is that nothing requires the atoms in an IRS to be located adjacently to one another, or even to form a surface! But they are probably easier to coordinate if they are in more or less the same place.
Cell-free Massive MIMO and Radio Stripes
I have recorded a popular science video that explains how a cell-free network architecture can provide major performance improvements over 5G cellular networks, and why radio stripes is a promising way to implement it:
If you want more technical details, I recommend our recent survey paper “Ubiquitous Cell-Free Massive MIMO Communications“. One of the authors, Dr. Hien Quoc Ngo at Queen’s University Belfast, has created a blog about Cell-free Massive MIMO. In particular, it contains a list of papers on the topic and links to the programming code of some of them.
Scalable Cell-Free Massive MIMO
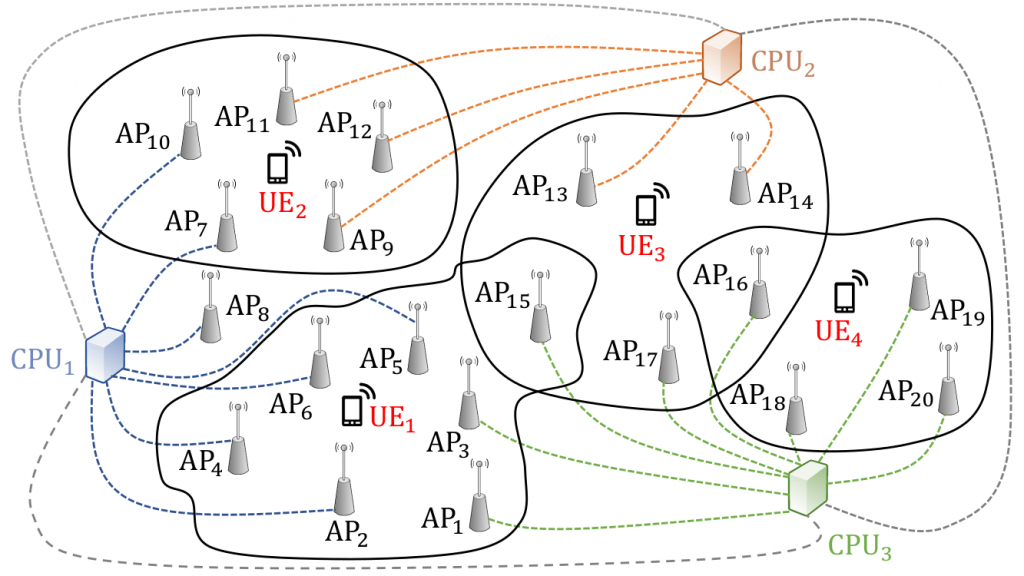
Cell-free massive MIMO is likely one of the technologies that will form the backbone of any xG with x>5. What distinguishes cell-free massive MIMO from distributed MIMO, network MIMO or cooperative multi-point (CoMP)? The short answer is that cell-free massive MIMO works, it can deliver uniformly good service throughout the coverage area, and it requires no prior knowledge of short-term CSI (just like regular cellular massive MIMO). A longer answer is here. The price to pay for this superiority, no shock, is the lack of scalability: for canonical cell-free massive MIMO there is a practical limit on how large the system can be, and this scalability concerns both the power control, the signal processing, and the organization of the backhaul.
At ICC this year we presented this approach towards scalable cell-free massive MIMO. A key insight is that power control is extremely vital for performance, and a scalable cell-free massive MIMO solution requires a scalable power control policy. No surprise, some performance must be sacrificed relative to canonical cell-free massive MIMO. Coincidentally, another paper in the same session (WC-26) also devised a power control policy with similar qualities!
Take-away point? There are only three things that matter for the design of cell-free massive MIMO signal processing algorithms and power control policies: scalability, scalability and scalability…
Signal Processing Makes it Work
Check out this video, produced by the IEEE Signal Processing Society’s Signal Processing for Communications and Networking (SPCOM) technical committee. The video explains to the layman what 5G is for, and how massive MIMO comes in…
Molecular MIMO at IEEE CTW-2019
One more reason to attend the IEEE CTW 2019: Participate in the Molecular MIMO competition! There is a USD 500 award to the winning team.
The task is to design a molecular MIMO communication detection method using datasets that contain real measurements. Possible solutions may include classic approaches (e.g., thresholding-based detection) as well as deep learning-based approaches.
More detail: here.