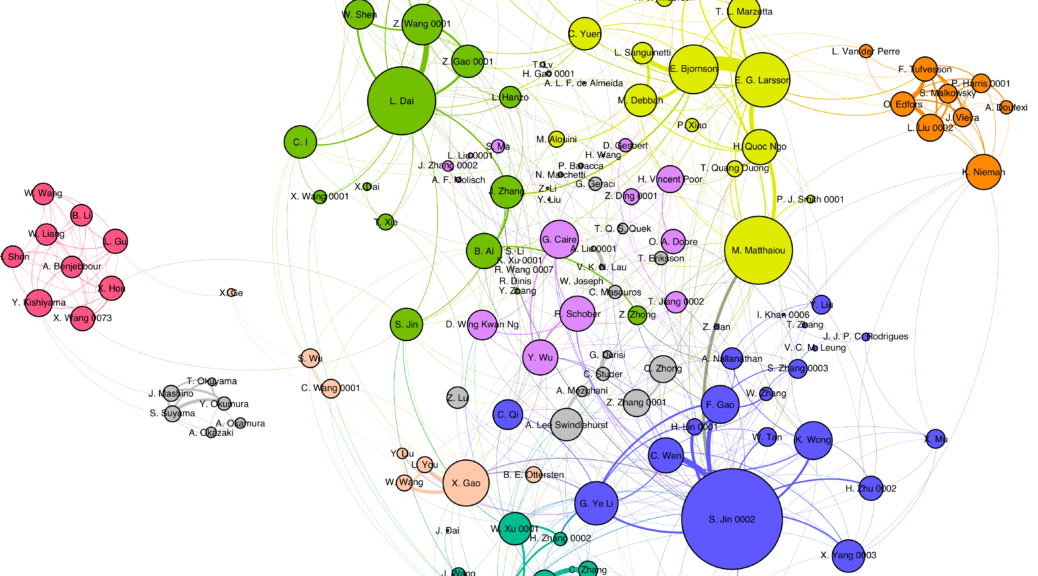
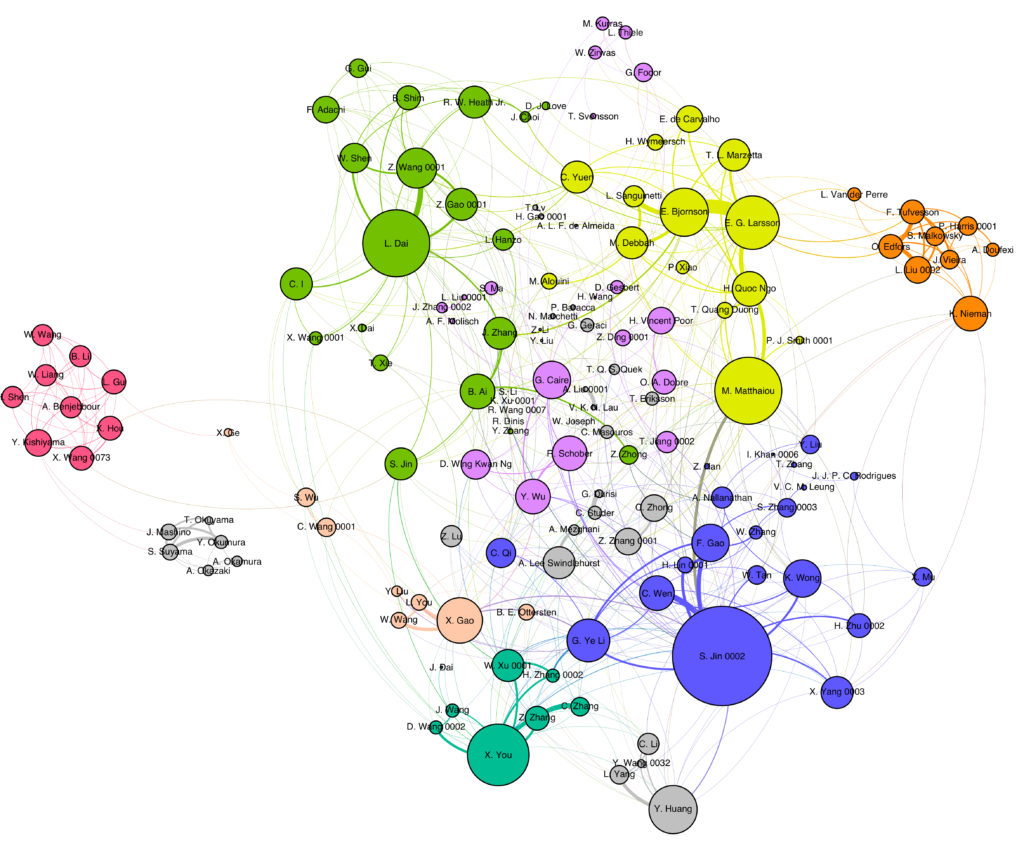
I have written several blog posts about how the hardware concepts of reconfigurable reflectarrays and metasurfaces are gaining interest in the wireless communication community, for example, to create a new type of full-duplex transparent relays. The technology is also known as reconfigurable intelligent surfaces and intelligent reflecting surfaces.
In my latest magazine paper, I identified real-time reconfigurability as the key technical research challenge: we need fast algorithms for over-the-air channel estimation that can handle large surfaces and complex propagation environments. In other words, we need hardware that can be reconfigured and algorithms to find the right configuration.
The literature contains several theoretical algorithms but it is a very different thing to demonstrate real-time reconfigurability in lab experiments. I was therefore impressed when finding the following video from the team of Dr. Mohsen Khalily at the University of Surrey:
The video shows how a metasurface is used to reflect a signal from a transmitter to a receiver. In the second half of the video, they move the receiver out of the reflected beam from the metasurface and then press a button to reconfigure the surface to change the direction of the beam.
I asked Dr. Khalily to tell me more about the setup:
“The metasurface consists of several conductive printed patches (scatterers), and the size of each scatterer is a small proportion of the wavelength of the operating frequency. The macroscopic effect of these scatterers defines a specific surface impedance and by controlling this surface impedance, the reflected wave from the metasurface sheet can be manipulated. Each individual scatterer or a cluster of them can be tuned in such a way that the whole surface can reconstruct radio waves with desired characteristics without emitting any additional waves.”
The surface shown in the video contains 2490 patches that are printed on a copper ground plane. The patches are made of a new micro-dispersed ceramic PTFE composite and designed to support a wide range of phase variations along with a low reflection loss for signals in the 3.5 GHz band. The design of the surface was the main challenge according to Dr. Khalily:
“Fabrication was very difficult due to the size of the surface, so we had to divide the surface into six tiles then attach them together. Our surface material has a higher dielectric constant than the traditional PTFE copper-clad laminates to meet the design and manufacturing of circuit miniaturization. This material also possesses high thermal conductivity, which gives an added advantage for heat dissipation of the apparatus.”

The transmitter and receiver were in the far-field of the metasurface in the considered experimental setup. Since there is an unobstructed line-of-sight path, it was sufficient to estimate the angular difference between the receiver and the main reflection angle, and then adjust the surface impedance to compensate for the difference. When this was properly done, the metasurface improved the signal-to-noise ratio (SNR) by almost 15 dB. I cannot judge how close this number is to the theoretical maximum. In the considered in-room setup with highly directional horn antennas at the transmitter and receiver, it might be enough that the reflected beam points in roughly the right direction to achieve a great SNR gain. I’m looking forward to learning more about this experiment when there is a technical paper that describes it.
This is not the first experiment of this kind, but I think it constitutes the state-of-the-art when it comes to bringing the concept of reconfigurable intelligent surfaces from theory to practice.