When T. Marzetta introduced the Massive MIMO concept in his seminal article from 2010, he concluded that “the phenomenon of pilot contamination impose[s] fundamental limitations on what can be achieved with a noncooperative cellular multiuser MIMO system.”
More precisely, he showed that the channel capacity under i.i.d. Rayleigh fading converges to a finite limit as the number of base stations goes to infinity. The value of this limit is determined by the interference level in the channel estimation phase. There are hundreds of papers on IEEEXplore that deals with the pilot contamination issue, trying to push the limit upwards or achieve higher performance for a given number of antennas. Various advanced mitigation methods have been developed to cure the symptoms of pilot contamination.
But was pilot contamination really a fundamental limitation to start with? In 2018, we published a paper called “Massive MIMO Has Unlimited Capacity” where we showed that there is an unexpectedly simple solution to the problem. You don’t need a sledgehammer to “crack the pilot contamination nut“, but the right combination of state-of-the-art tools will do. While I have written about this in previous blog posts and briefly mentioned it in videos, I have finally recorded a comprehensive lecture on the topic. It is 82 minutes long and was given online by invitation from Hacettepe University, Turkey. No previous knowledge on the topic is required. I hope you will enjoy it in small or big doses!
We have now released the third episode of the podcast Wireless Future, with the following abstract:
The research towards 6G has already been initiated. One of the most hyped concepts in the research community is “reconfigurable intelligent surfaces”, which can be utilized to create smart walls that capture wireless signals and reflect them towards the user device. In this episode, Erik G. Larsson and Emil Björnson discuss the prospects and limitations of this new technology. Is it the next big thing in wireless? To learn more, they recommend their new overview article “Reconfigurable Intelligent Surfaces: Three Myths and Two Critical Questions”, to appear in IEEE Communications Magazine, which can be downloaded at https://arxiv.org/pdf/2006.03377.
You can watch the video podcast on YouTube:
You can listen to the audio-only podcast at the following places:
5G used to be described as synonymous with millimeter-wave communications, but now when 5G networks are being rolled out all around the world, the focus is instead on Massive MIMO in the 3 GHz band. Moreover, millimeter-wave communications used to be synonymous with hybrid beamforming (e.g., using multiple analog phased arrays), often described as a necessary compromise between performance and hardware complexity. However, digital implementations are already on the way.
Last year, I wrote about experiments by NEC with a 24-antenna base station that carries out digital beamforming in the 28 GHz band. The same convergence towards digital solutions is happening for the chips that can be used in 5G terminals. The University of Michigan published experimental results at the 2020 IEEE Radio Frequency Integrated Circuits Symposium (RFIC) regarding a 16-element prototype for the 28 GHz band. The university calls it the “first digital single-chip millimeter-wave beamformer“. It is manufactured as a single chip using 40 nm CMOS technology and has a dimension of around 3 x 3 mm. The chip doesn’t include the 16 antenna elements (which are connected to it, see the image below and click on it to find larger images) but transceiver chains with low-noise amplifiers, phase-locked loops, analog-to-digital converters (ADCs), etc. While each antenna element has a separate ADC, groups of four adjacent ADCs are summing up their digital signals before they reach the baseband processor. Hence, from a MIMO perspective, this is essentially a digital four-antenna receiver.
One reason to call this a prototype rather than a full-fleshed solution is that the chip can only function as a receiver, but this doesn’t take away the fact that this is an important step forward. In an interview with the Michigan Engineering News Center, Professor Michael P. Flynn (who lead the research) is explaining that “With analog beamforming, you can only listen to one thing at a time” and “This chip represents more than seven years of work by multiple generations of graduate students”.
Needless to say, the first 5G base stations and cell phones that support millimeter-wave bands will make use of hybrid beamforming architectures. For example, the Ericsson Street Macro 6701 (that Verizon is utilizing in their network) contains multiple phased arrays, which can take 4 inputs and thereby produce up to 4 simultaneous beams. However, while the early adopters are making use of hybrid architectures, it becomes increasingly likely that fully digital architectures will be available when millimeter-wave technology becomes more widely adopted around the world.
We have now released the second episode of the podcast Wireless Future, with the following abstract:
There are often hypes and speculations around new wireless technologies, including “Massive MIMO”, which is the key new feature in 5G. In 2015, Emil Björnson and Erik G. Larsson wrote the article “Massive MIMO: Ten Myths and One Critical Question” together with Thomas Marzetta. It was an attempt to dispel some of the misconceptions that were floating around at the time. In this episode, they look back at the statements they claimed to be myths to see if they were right and whether the myths are still around. The article received the 2019 Fred W. Ellersick Prize from the IEEE Communications Society and can be downloaded at https://arxiv.org/pdf/1503.06854.
You can watch the video podcast on YouTube:
You can listen to the audio-only podcast at the following places:
Like many other teachers, I had to quickly switch from physical teaching to online mode at the beginning of the COVID-19 pandemic. I am normally giving lectures in a course called Multiple Antenna Communications in the period March to May. It is a luxury to teach this course since there are only 5-10 students and these have actively selected the course so they are truly interested in the topic!
Since I was anyway going to give online lectures, I was thinking: Why not record them in a way that other people could also benefit from them? I normally give 2-hour lectures where I switch between presenting PowerPoint slides and giving examples on the whiteboard; for example, I might make a theoretical derivation on the board and then summarize it on a slide and show simulation results. This time, I decided to decouple these activities by creating one video per lecture that the students could watch in advance, and then I had live sessions where I went through prepared examples and answered questions. This was done by sharing my screen and write the examples into OneNote using a simple drawing pad, which isn’t so much different from writing on a whiteboard.
I think this online teaching approach was quite successful. I am quite satisfied with the 12 lecture videos that I created, which consist of a total of 8 hours of narrated slides. The first video has more than 6000 views on YouTube, which is three orders-of-magnitude more than the number of students that I had in the course. I received many requests for the slides, so I uploaded them to GitHub.
Here is the video series in its entirety:
I will keep these resources available. If you are a teacher, please feel free to reuse the videos or slides in your teaching! I hope that the efforts that I and other teachers put into producing online content during the pandemic can be utilized to aid the learning of students also in the years to come.
I am excited to announce the new podcast “Wireless Future“, where Emil Björnson and Erik G. Larsson are discussing current and future wireless technologies, as well as their impact on society. Each episode will focus on a particular topic and be available in two formats: A video podcast on YouTube and an audio-only podcast that can be downloaded from the major podcast apps (there is a list below). We intend to release one episode every other week, starting from today. We hope you will enjoy it! Please send us feedback, questions, and suggestions on future topics to podcast@ebjornson.com.
Episode 1: Massive MIMO: Where do we stand?
In the first episode of “Wireless Future”, Erik G. Larsson and Emil Björnson talk about the brand new 5G networks and what role the technology component “Massive MIMO” is playing. They reflect upon whether the practical implementation of the technology became as they envisioned in their textbooks “Fundamentals of Massive MIMO” and “Massive MIMO Networks”.
You can listen to the audio-only podcast at the following places:
When researchers study the basic properties of multi-antenna technologies, it is a common practice to model the channels using independent and identically distributed (i.i.d.) Rayleigh fading. This practice goes back many decades and is convenient since: 1) every antenna observes an independent realization of the channel; 2) each antenna is statistically equally good, so the ordering doesn’t matter; 3) the channel coefficients are complex Gaussian distributed, which leads to convenient mathematics.
The i.i.d. Rayleigh fading model has become the baseline that is considered unless the research is explicitly focused on a different model. When using the model to study spatial diversity, the diversity gain becomes proportional to the number of antennas. When characterizing the ergodic capacity of Massive MIMO, one can derive simple closed-form bounds where the SINR is proportional to the number of antennas. Both results are correct, but their generality is limited by the generality of the underlying fading model. Hence, it is important to know under what conditions i.i.d. Rayleigh fading can be observed.
When i.i.d. fading might occur
In isotropic scattering environments, where the multi-path components are uniformly distributed over all directions (in three dimensions), the fading realizations observed at two points have a correlation determined by the distance d between them. More precisely, the cross-correlation is sinc(2d/λ), where λ is the wavelength. The sinc function is zero when the argument is a non-zero integer, thus the fading realizations at two different points are uncorrelated if and only if they are separated by an integer multiple of λ/2. For example, d =λ/2, λ, 3λ/2, etc. Since the channel coefficients are Gaussian distributed in isotropic fading, uncorrelated fading results in independent fading.
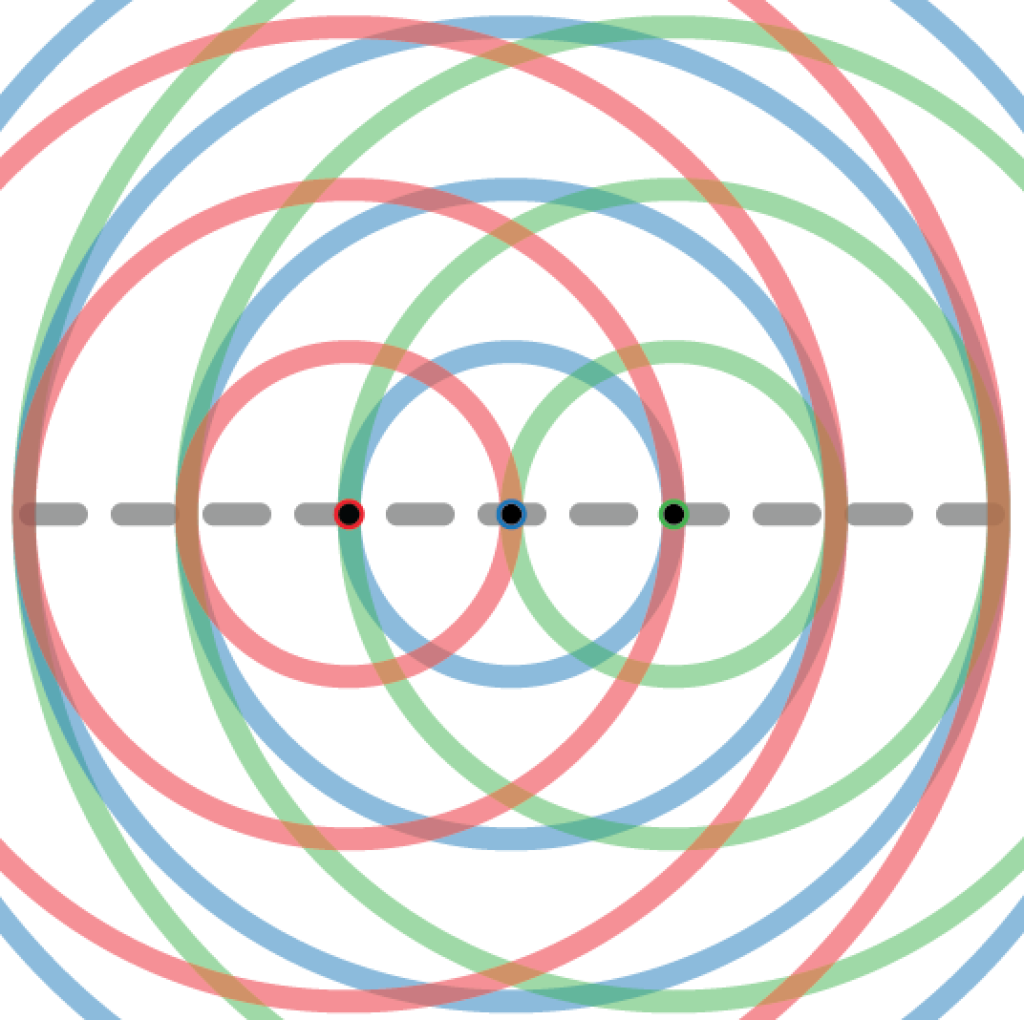
The figure above illustrates a setup where 3 antennas are deployed on the dashed line with a separation of λ/2. The red circles around the “red antenna” show at which locations one can observe fading realizations that are independent of the observation made at the red antenna. The circles have radius λ/2, λ, 3λ/2, etc. The blue and green circles have the same meanings for the blue and green antennas, respectively. Since all the antennas are deployed on the circles of the other antennas, they will observe mutually uncorrelated (independent) fading. This will give rise to i.i.d. Rayleigh fading.
Suppose we want to deploy a fourth antenna. To retain an i.i.d. fading distribution, we must put it at a point where a red, a blue, and a green circle intersect. As indicated by the figure, such points are only be found along the dashed line. Hence, a uniform linear array (ULA) with λ/2-separation between the adjacent antennas will observe i.i.d. fading if deployed in an isotropic scattering environment.
When i.i.d. fading cannot occur
Apart from the ULA example, there is essentially no other case where i.i.d. fading can occur. This is important since two-dimensional planar arrays are becoming standard, for example, when deploying Massive MIMO in cellular networks. Even if we allow ourselves to deviate from the isotropic scattering assumption, any physically accurate stochastic channel model for planar arrays exhibits correlation. This is proved in the paper “Spatially-Stationary Model for Holographic MIMO Small-Scale Fading“.
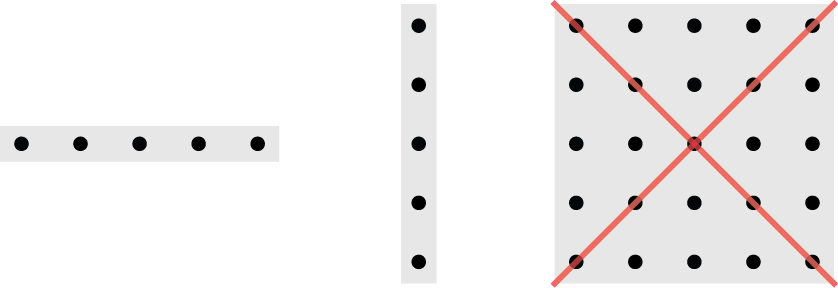
The horizontal and vertical ULAs in the figure above can observe i.i.d. fading, while the planar array cannot; even if the horizontal and vertical antenna spacing is λ/2, the spacings along the diagonals are different.
Looking further into the future, two new array concepts are currently receiving attention from the research community:
Large intelligent surfaces (LIS);
Reconfigurable intelligent surfaces (RIS).
LIS are large active arrays, while RIS are large passive arrays with elements that scatter incident signals in a semi-controllable fashion. In both cases, the word “surface” signifies that at a planar array, or even a three-dimensional array, is considered. Hence, these arrays can never observe i.i.d. fading—it is physically impossible. Moreover, a key characteristic of LIS and RIS is that the element spacing is smaller than λ/2 (to approximate a continuously controllable surface), which is yet another reason for obtaining spatial channel correlation. It is therefore worrying that several early papers on these topics are making use of the i.i.d. fading model: the analysis might be beautiful but the results are insignificant since they cannot be observed in practice.
The way forward
Even if we have reached the end of the road for the i.i.d. Rayleigh fading model, we don’t have to wander into the darkness. We just need to switch to utilizing the more general spatially correlated Rayleigh fading model. There is already a rich literature on how to design communication systems for such channels. My book “Massive MIMO networks” is one possible starting point, but not the only one.
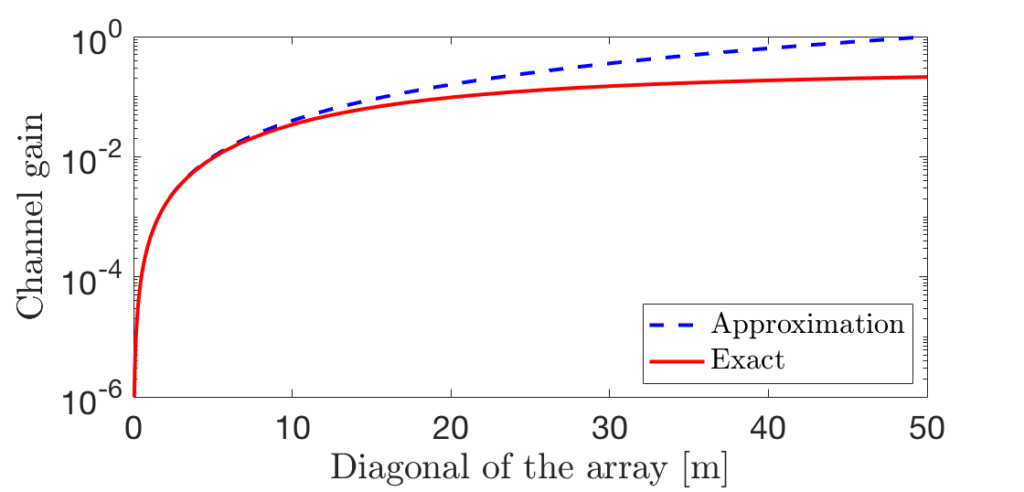
To make the transition to physically accurate models easier, I have co-authored the paper “Rayleigh Fading Modeling and Channel Hardening for Reconfigurable Intelligent Surfaces“, which derives a spatial correlation model for LIS and RIS in isotropic scattering environments. It can take the role as the new baseline channel model that is used when no other specific channel model is studied. We also elaborate on why the classical “Kronecker approximation” of spatial correlation matrices is inaccurate; for example, it results in i.i.d. fading also for planar arrays.
